 /
/ 
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 425 点
問題文
H 行 W 列のマス目があります。上から i 行目 (1\leq i\leq H)、左から j 列目 (1\leq j\leq W) のマスをマス (i,j) と呼ぶことにします。
はじめ、マス (i,j) は S_{i,j} が # のとき黒、. のとき白で塗られています。
以下の操作を 10^{100} 回行います。
- 白で塗られているマスであって、そのマスに辺で隣接するマスのうちちょうど 1 つが黒で塗られているようなマスの集合を T とする。T の各マスに対して、そのマスを黒で塗る。ただし、2 つのマス (i_1,j_1),(i_2,j_2) が辺で隣接するとは、 |i_1-i_2|+|j_1-j_2|=1 であることをいう。
すべての操作が終わったあとに黒く塗られているマスの個数を求めてください。
制約
- 2\leq H,W
- HW\leq 3\times 10^5
- H,W は整数
- S_{i,j} は
#または.
入力
入力は以下の形式で標準入力から与えられる。
H W
S_{1,1}S_{1,2}\ldots S_{1,W}
S_{2,1}S_{2,2}\ldots S_{2,W}
\vdots
S_{H,1}S_{H,2}\ldots S_{H,W}
出力
答えを出力せよ。
入力例 1
9 9 ......... ......... ......... ......... ....#.... ......... ......... ......... .........
出力例 1
57
操作によってマス目は以下のように変化します。(上の数字は操作回数を表しており、10 回目の操作後まで表示しています。)
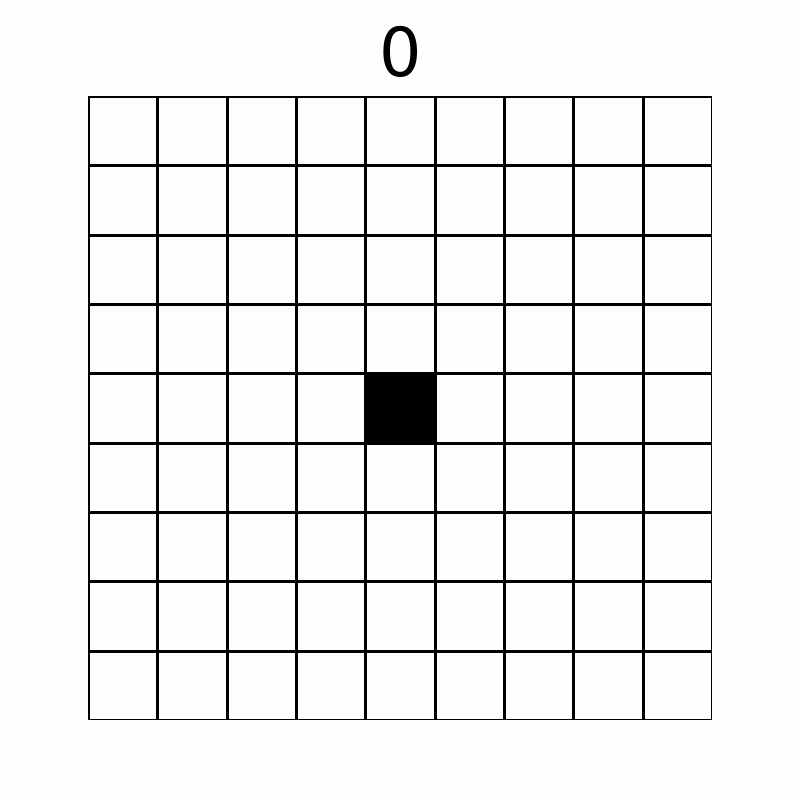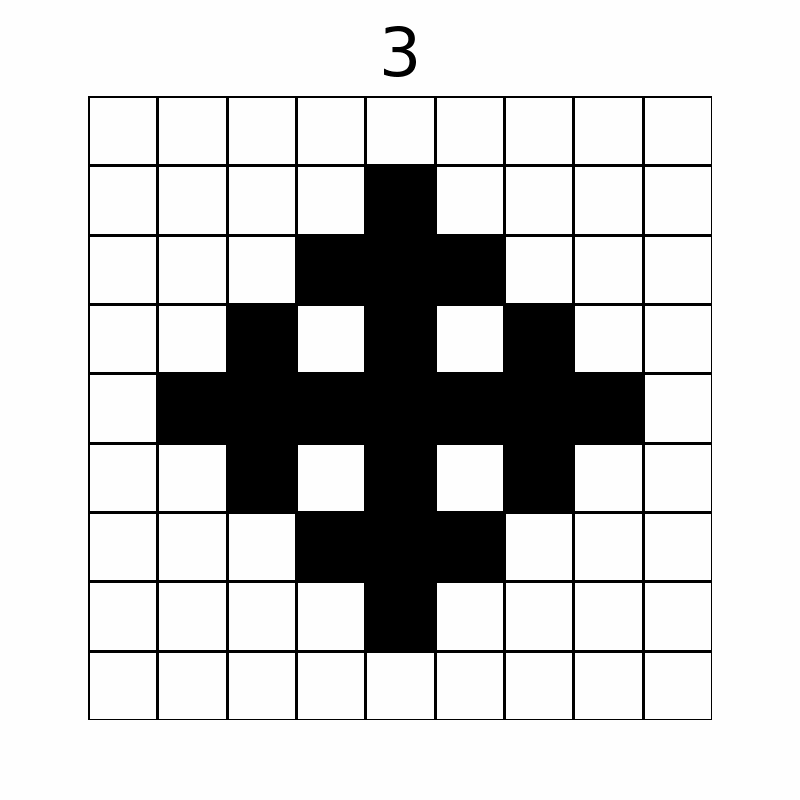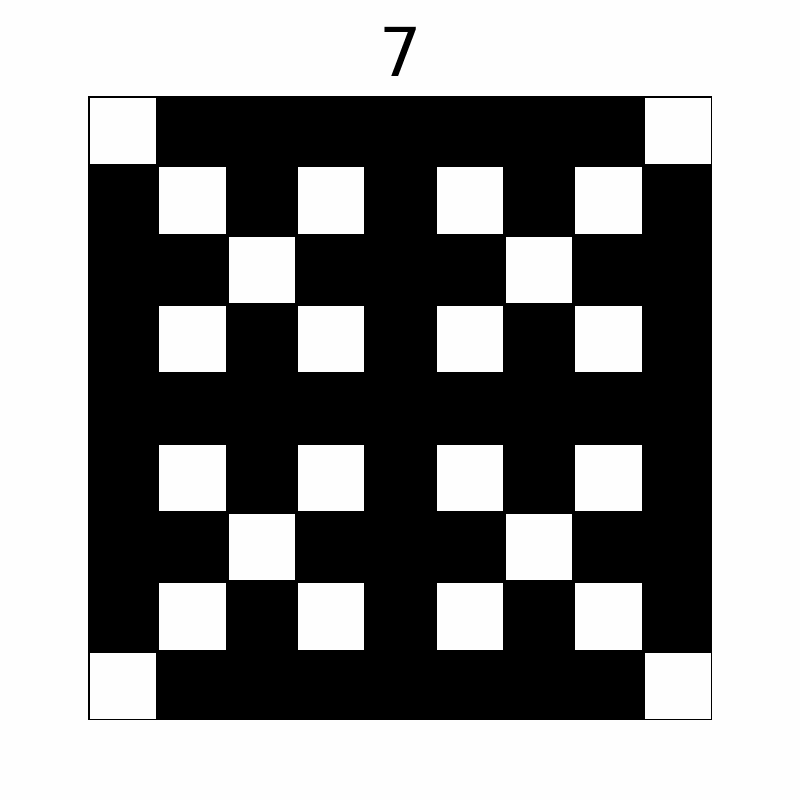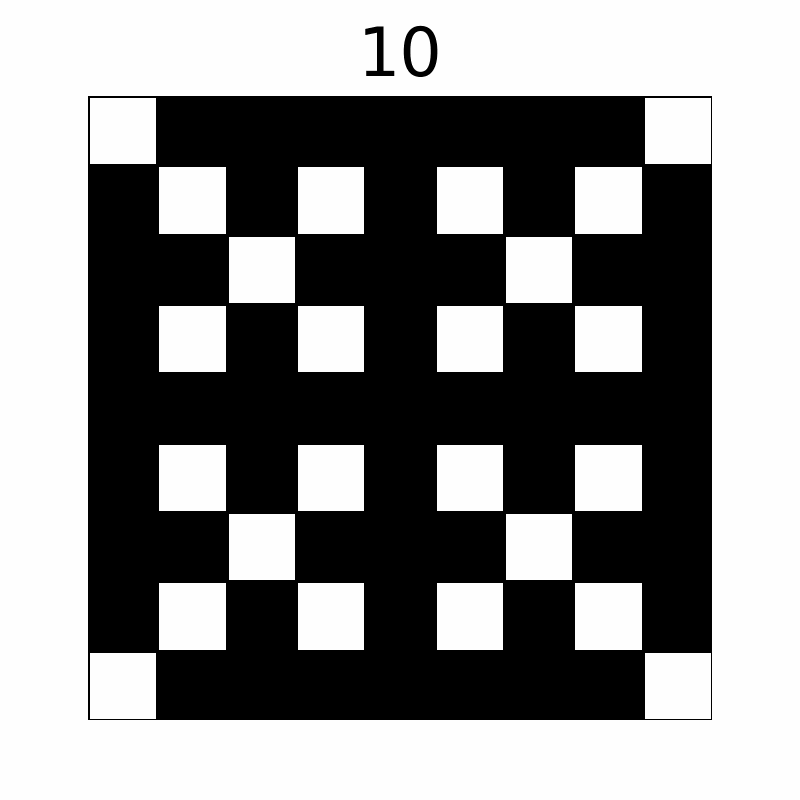
最終的に黒く塗られたマスは 57 個です。
入力例 2
2 2 .. ..
出力例 2
0
入力例 3
10 10 .......... ....#..... #.......#. ......#... .......#.. .....#.... .......... .......... ..#...#... .......#..
出力例 3
64
Score : 425 points
Problem Statement
There is a grid with H rows and W columns. We call the cell at the i-th row from the top (1\leq i\leq H) and j-th column from the left (1\leq j\leq W) as cell (i,j).
Initially, cell (i,j) is colored black if S_{i,j} is # and white if it is ..
Perform the following operation 10^{100} times:
- Let T be the set of cells that are colored white and have exactly one adjacent cell colored black. Color each cell in T black. Here, two cells (i_1,j_1) and (i_2,j_2) are adjacent if and only if |i_1-i_2|+|j_1-j_2|=1.
Find the number of cells that are colored black after all operations are completed.
Constraints
- 2\leq H,W
- HW\leq 3\times 10^5
- H and W are integers.
- S_{i,j} is
#or..
Input
The input is given from Standard Input in the following format:
H W
S_{1,1}S_{1,2}\ldots S_{1,W}
S_{2,1}S_{2,2}\ldots S_{2,W}
\vdots
S_{H,1}S_{H,2}\ldots S_{H,W}
Output
Output the answer.
Sample Input 1
9 9 ......... ......... ......... ......... ....#.... ......... ......... ......... .........
Sample Output 1
57
The grid changes as follows through the operations. (The number above represents the operation count. The first ten operations are displayed.)
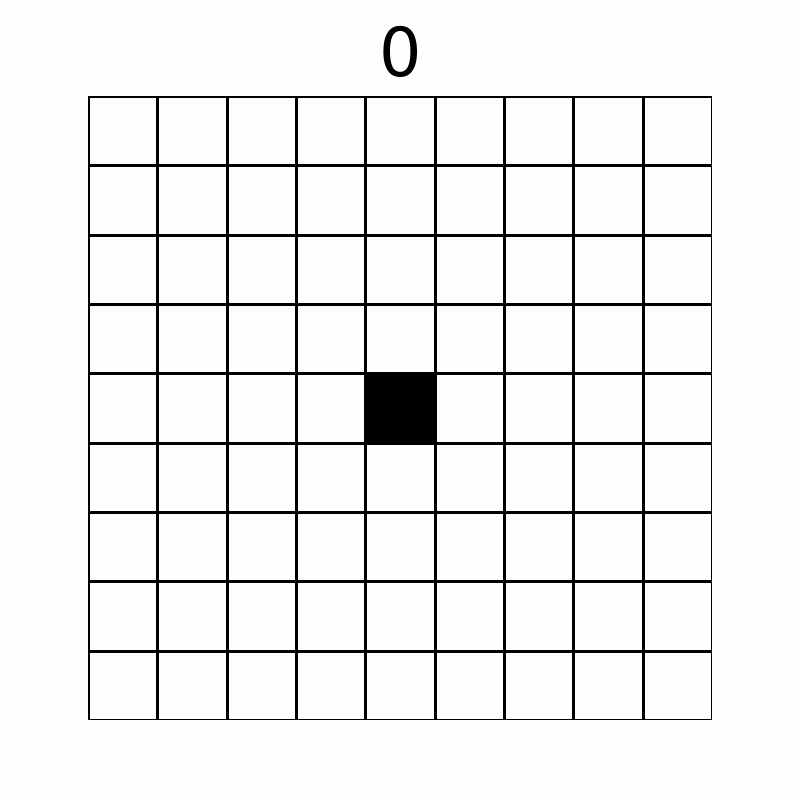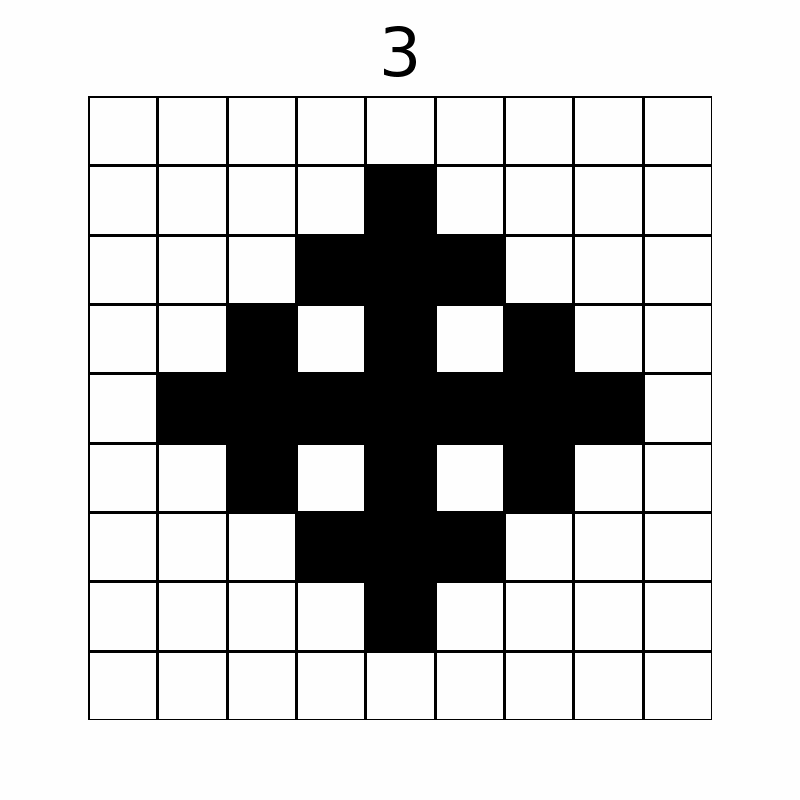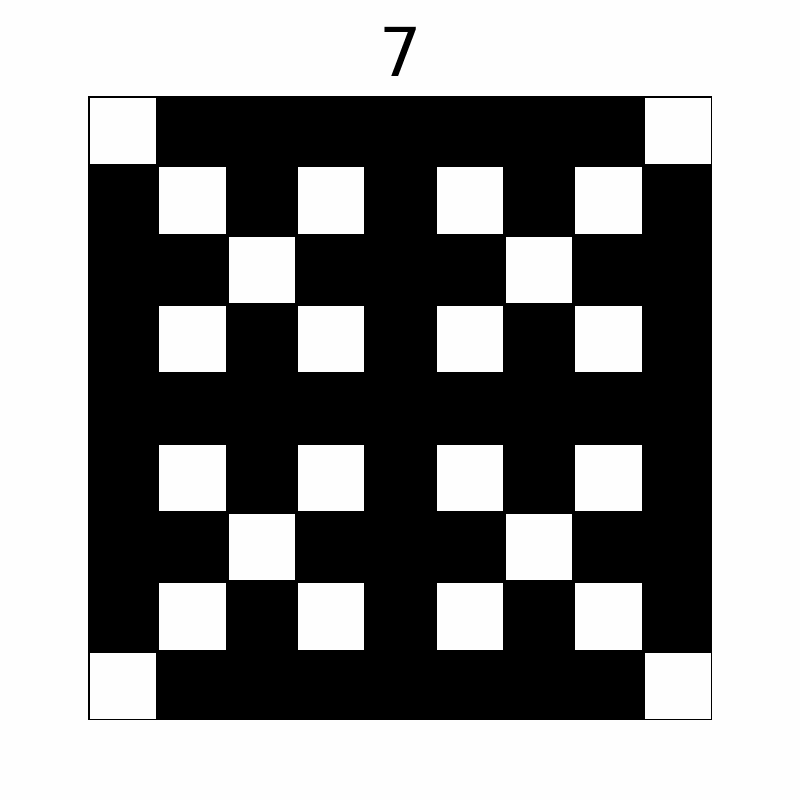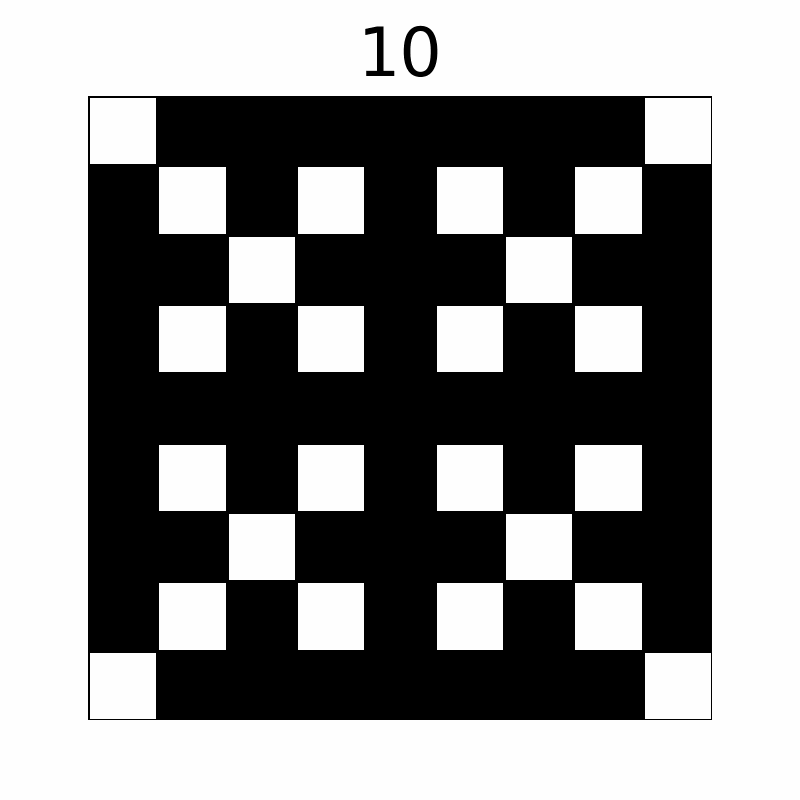
Eventually, 57 cells are colored black.
Sample Input 2
2 2 .. ..
Sample Output 2
0
Sample Input 3
10 10 .......... ....#..... #.......#. ......#... .......#.. .....#.... .......... .......... ..#...#... .......#..
Sample Output 3
64