 /
/ 
Time Limit: 3 sec / Memory Limit: 1024 MiB
配点 : 525 点
問題文
円周上に等間隔に N 個の点があり、時計回りに 1,2,\dots,N と番号がついています。
以下の形式のクエリが Q 個与えられるので順に処理してください。
- 点 A_i と点 B_i を結ぶ線分を書く。ただし、この線分が既に書かれている線分と交わる場合は書かない。
ここで、2Q 個の整数 A_1,\ldots,A_Q,B_1,\ldots,B_Q は相異なることが保証されます。
各線分が書かれたかどうか答えてください。
制約
- 2 \leq N \leq 10^6
- 1 \leq Q \leq 3\times 10^5
- 1 \leq A_i < B_i \leq N
- 2Q 個の整数 A_1,\ldots,A_Q,B_1,\ldots,B_Q は相異なる
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
N Q A_1 B_1 A_2 B_2 \vdots A_Q B_Q
出力
Q 行出力せよ。
i 行目には、i 番目のクエリにおいて線分が書かれたとき Yes、書かれなかったとき No と出力せよ。
入力例 1
8 3 1 5 2 7 3 4
出力例 1
Yes No Yes
クエリにより図のように線分が書かれます。
- 1 番目のクエリで、点 1 と点 5 を結ぶ線分が書かれる。
- 2 番目のクエリで、点 2 と点 7 を結ぶ線分は、1 番目のクエリで書いた線分と交わるので書かない。
- 3 番目のクエリで、点 3 と点 4 を結ぶ線分が書かれる。
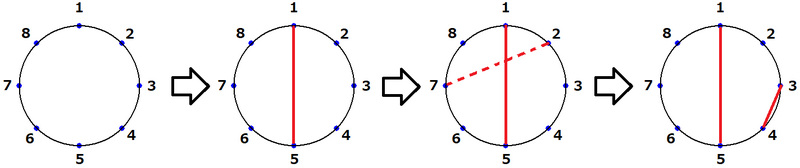
入力例 2
999999 4 123456 987654 888888 999999 1 3 2 777777
出力例 2
Yes No Yes No
Score : 525 points
Problem Statement
There are N points equally spaced on a circle, numbered 1,2,\dots,N clockwise.
You are given Q queries of the following form; process them in order.
- Draw the line segment connecting points A_i and B_i. However, if this segment intersects a segment that has already been drawn, do not draw it.
Here, it is guaranteed that the 2Q integers A_1,\ldots,A_Q,B_1,\ldots,B_Q are all distinct.
For each query, answer whether the segment was drawn.
Constraints
- 2 \leq N \leq 10^6
- 1 \leq Q \leq 3\times 10^5
- 1 \leq A_i < B_i \leq N
- The 2Q integers A_1,\ldots,A_Q,B_1,\ldots,B_Q are pairwise distinct.
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N Q A_1 B_1 A_2 B_2 \vdots A_Q B_Q
Output
Output Q lines.
On the i-th line, output Yes if, in the i-th query, the segment was drawn, and No if it was not drawn.
Sample Input 1
8 3 1 5 2 7 3 4
Sample Output 1
Yes No Yes
By the queries, the segments are drawn as in the figure.
- In the 1-st query, the segment connecting points 1 and 5 is drawn.
- In the 2-nd query, the segment connecting points 2 and 7 is not drawn because it intersects the segment drawn in the 1-st query.
- In the 3-rd query, the segment connecting points 3 and 4 is drawn.

Sample Input 2
999999 4 123456 987654 888888 999999 1 3 2 777777
Sample Output 2
Yes No Yes No