 /
/ 
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 500 点
問題文
N 頂点 M 辺の連結無向グラフがあります。 頂点には頂点 1, 頂点 2,\ldots, 頂点 N と番号付けられており、i 番目 (1\le i\le M) の辺は頂点 u _ i と頂点 v _ i を結んでいます。
i=1,2,\ldots,N について次の問題を解いてください。
はじめ、高橋くんの体重は 0 です。
高橋くんは、車に乗って頂点 1 に訪れ、頂点 i に向かって移動を行います。 高橋くんが頂点 v\ (1\le v\le N) に訪れるとき、高橋くんの体重は W _ v だけ増加します。
高橋くんが乗っている車は辺に沿って移動することができます。 高橋くんが辺を通過するとき、そのときの高橋くんの体重を X として、車は燃料を X 消費します。
高橋くんが頂点 i にたどり着くために消費する燃料の量の最小値を求めてください。
制約
- 1\le N\le5000
- 1\le M\le5000
- 1\le W _ i\le10 ^ 9\ (1\le i\le N)
- 1\le u _ i\le v _ i\le N\ (1\le i\le M)
- 与えられるグラフは連結
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N M W _ 1 W _ 2 \ldots W _ N u _ 1 v _ 1 u _ 2 v _ 2 \vdots u _ M v _ M
出力
N 行にわたって出力せよ。 i 行目 (1\le i\le N) には、高橋くんが頂点 i にたどり着くのに必要な燃料の量を出力せよ。
入力例 1
5 6 3 1 4 1 5 1 2 1 3 2 3 2 4 3 5 4 5
出力例 1
0 3 3 7 10
与えられたグラフは以下のようになります。
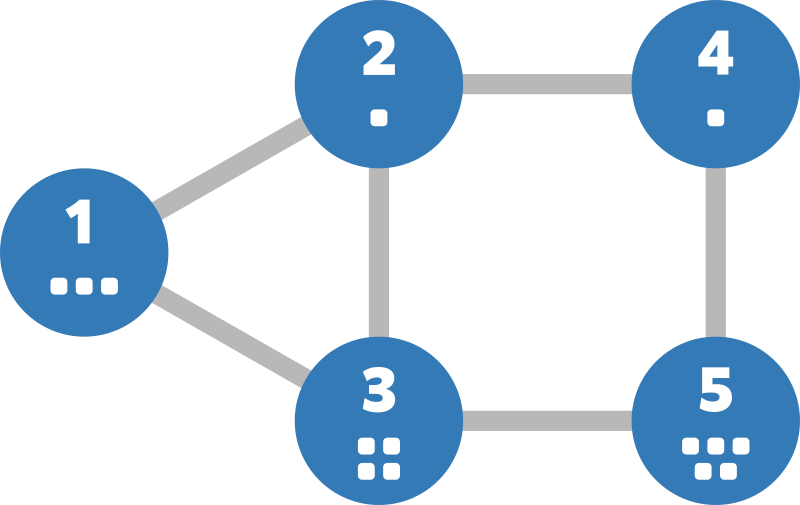
例えば、高橋くんは頂点 1 に訪れてから次のように行動することで頂点 5 にたどり着くことができます。
- 高橋くんが頂点 1 に訪れる。高橋くんの体重が 3 増加し、3 になる。
- 高橋くんが燃料を 3 消費して頂点 3 に移動する。高橋くんの体重が 4 増加し、7 になる。
- 高橋くんが燃料を 7 消費して頂点 5 に移動する。高橋くんの体重が 5 増加し、12 になる。
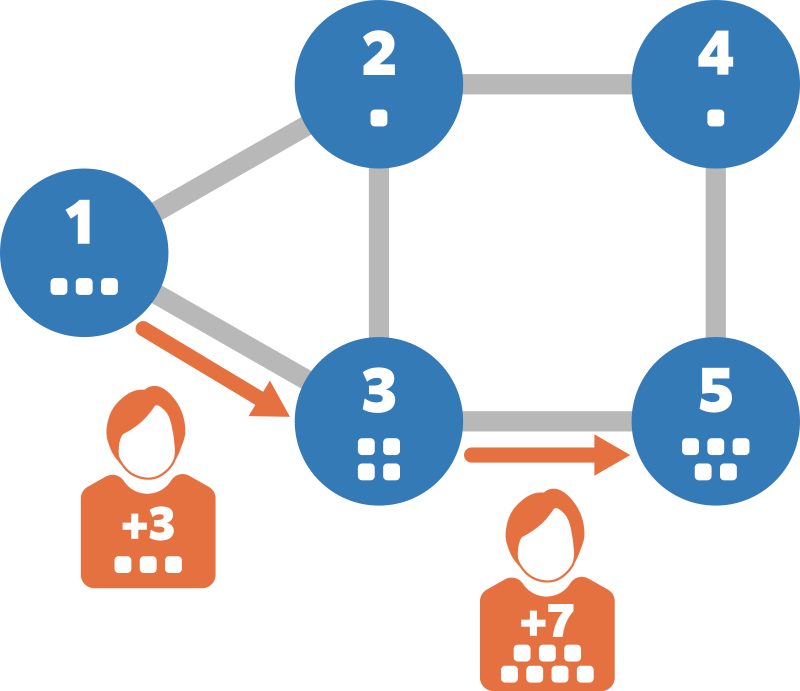
このように行動することで燃料を 10 だけ消費して頂点 5 にたどり着くことができます。 消費する燃料を 9 以下にすることはできないため、5 行目には 10 を出力してください。
入力例 2
5 4 1000000000 1000000000 1000000000 1000000000 1000000000 1 2 2 3 3 4 4 5
出力例 2
0 1000000000 3000000000 6000000000 10000000000
答えが 2 ^ {32} を越える場合があることに注意してください。
入力例 3
10 20 74931 58277 33783 91022 53003 11085 65924 63548 78622 77307 1 8 3 6 5 10 4 6 1 3 1 7 2 6 7 10 8 9 3 4 4 4 4 6 6 6 5 10 1 7 4 5 1 2 3 7 2 3 5 8
出力例 3
0 74931 74931 183645 213410 183645 74931 74931 213410 215786
Score : 500 points
Problem Statement
There is a connected undirected graph with N vertices and M edges. The vertices are numbered vertex 1, vertex 2,\ldots, vertex N, and the i-th edge (1\le i\le M) connects vertices u _ i and v _ i.
For i=1,2,\ldots,N, solve the following problem:
Initially, Takahashi's weight is 0.
He travels by car to visit vertex 1 and moves toward vertex i. When he visits vertex v\ (1\le v\le N), his weight increases by W _ v.
The car he is riding can move along the edges. When he passes through an edge, letting X be his weight at that time, the car consumes X fuel.
Find the minimum amount of fuel consumed for him to reach vertex i.
Constraints
- 1\le N\le5000
- 1\le M\le5000
- 1\le W _ i\le10 ^ 9\ (1\le i\le N)
- 1\le u _ i\le v _ i\le N\ (1\le i\le M)
- The given graph is connected.
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N M W _ 1 W _ 2 \ldots W _ N u _ 1 v _ 1 u _ 2 v _ 2 \vdots u _ M v _ M
Output
Output over N lines. On the i-th line (1\le i\le N), output the amount of fuel needed for Takahashi to reach vertex i.
Sample Input 1
5 6 3 1 4 1 5 1 2 1 3 2 3 2 4 3 5 4 5
Sample Output 1
0 3 3 7 10
The given graph is as follows:

For example, Takahashi can reach vertex 5 by visiting vertex 1 and then acting as follows:
- He visits vertex 1. His weight increases by 3, becoming 3.
- He consumes 3 fuel to move to vertex 3. His weight increases by 4, becoming 7.
- He consumes 7 fuel to move to vertex 5. His weight increases by 5, becoming 12.

By acting this way, he can reach vertex 5 by consuming 10 fuel. It is impossible to reduce the fuel consumption to 9 or less, so output 10 on the 5th line.
Sample Input 2
5 4 1000000000 1000000000 1000000000 1000000000 1000000000 1 2 2 3 3 4 4 5
Sample Output 2
0 1000000000 3000000000 6000000000 10000000000
Note that the answer may exceed 2 ^ {32}.
Sample Input 3
10 20 74931 58277 33783 91022 53003 11085 65924 63548 78622 77307 1 8 3 6 5 10 4 6 1 3 1 7 2 6 7 10 8 9 3 4 4 4 4 6 6 6 5 10 1 7 4 5 1 2 3 7 2 3 5 8
Sample Output 3
0 74931 74931 183645 213410 183645 74931 74931 213410 215786