 /
/ 
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 425 点
問題文
無限に広いグリッドがあります。グリッドのあるマスはマス (0,0) と名前がついています。
マス (0,0) から下に r マス、右に c マスの移動した位置にあるマスをマス (r,c) と呼びます。
ここで、「下に r マス移動する」は r が負のときは「上に |r| マス移動する」ことを表し、「右に c マス移動する」は c が負のときには「左に |c| マス移動する」ことを表すものとします。
具体的には、マス (0,0) の周辺にあるマスは以下のようになります。
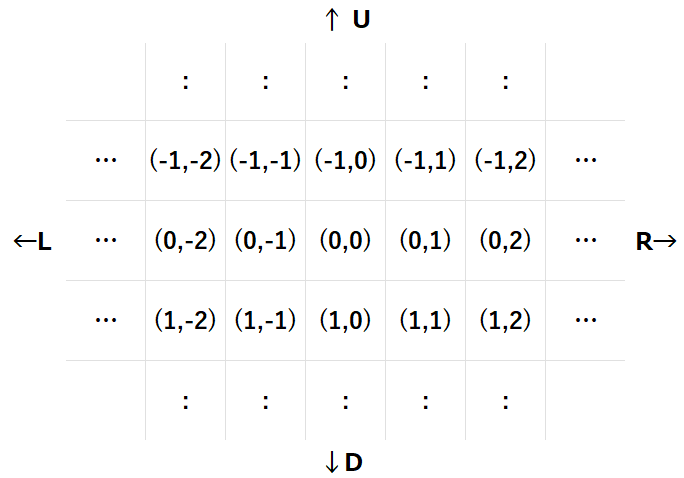
最初、高橋君はマス (R_t,C_t) に、青木君はマス (R_a,C_a) にいます。二人はそれぞれ U,D,L,R からなる長さ N の文字列 S,T に従って N 回移動を行います。
各 i について、高橋君と青木君の i 回目の移動は同時に行われます。具体的には、高橋君は S の i 文字目が U のとき上、D のとき下、L のとき左、R のとき右へ 1 マス移動し、青木君は T の i 文字目によって同様に移動します。
N 回の移動の中で、移動直後に高橋君と青木君が同じマスにいた回数を求めてください。
ただし、N は非常に大きいため S,T は ( (S'_1, A_1),\ldots(S'_M,A_M) ), ( (T'_1,B_1),\ldots,(T'_L,B_L) ) の形で与えられ、 S は「文字 S'_1 を A_1 個、\dots、文字 S'_M を A_M 個」をこの順に連結した文字列であり、T も同様です。
制約
- -10^9 \leq R_t,C_t,R_a,C_a \leq 10^9
- 1\leq N \leq 10^{14}
- 1\leq M,L \leq 10^5
- S'_i,T'_i は
U,D,L,Rのいずれか - 1 \leq A_i,B_i \leq 10^9
- A_1+\dots+A_M=B_1+\dots+B_L=N
- 与えられる数値は全て整数
入力
入力は以下の形式で標準入力から与えられる。
R_t C_t R_a C_a N M L S'_1 A_1 \vdots S'_M A_M T'_1 B_1 \vdots T'_L B_L
出力
答えを出力せよ。
入力例 1
0 0 4 2 3 2 1 R 2 D 1 U 3
出力例 1
1
このケースでは S= RRD、T= UUU であり、移動は次のように行われます。
- 最初、高橋君はマス (0,0) に、青木君はマス (4,2) にいる。
- 1 回目の移動後、高橋君はマス (0,1)、青木君はマス (3,2) にいる。
- 2 回目の移動後、高橋君はマス (0,2)、青木君はマス (2,2) にいる。
- 3 回目の移動後、高橋君はマス (1,2)、青木君はマス (1,2) にいる。
よって、高橋君と青木君が移動直後に同じマスにいた回数は 1 です。
入力例 2
1000000000 1000000000 -1000000000 -1000000000 3000000000 3 3 L 1000000000 U 1000000000 U 1000000000 D 1000000000 R 1000000000 U 1000000000
出力例 2
1000000001
2000000000 回目の移動から 3000000000 回目の移動までの 1000000001 回で高橋君と青木君は移動直後に同じマスにいます。
入力例 3
3 3 3 2 1 1 1 L 1 R 1
出力例 3
0
入力例 4
0 0 0 0 1 1 1 L 1 R 1
出力例 4
0
Score : 425 points
Problem Statement
There is an infinitely large grid. One cell of the grid is named cell (0,0).
The cell located r cells down and c cells right from cell (0,0) is called cell (r,c).
Here, "r cells down" means "|r| cells up" when r is negative, and "c cells right" means "|c| cells left" when c is negative.
Specifically, the cells around cell (0,0) are as follows:

Initially, Takahashi is at cell (R_t,C_t) and Aoki is at cell (R_a,C_a). They will each make N moves according to strings S and T of length N consisting of U, D, L, R.
For each i, Takahashi's and Aoki's i-th moves occur simultaneously: Takahashi moves one cell up if the i-th character of S is U, down if D, left if L, and right if R; Aoki moves similarly according to the i-th character of T.
Find the number of times Takahashi and Aoki are at the same cell immediately after a move during the N moves.
Since N is very large, S and T are given in the form ((S'_1, A_1),\ldots,(S'_M,A_M)) and ((T'_1,B_1),\ldots,(T'_L,B_L)), where S is the string obtained by concatenating "A_1 copies of character S'_1, \dots, A_M copies of character S'_M" in this order, and T is given similarly.
Constraints
- -10^9 \leq R_t,C_t,R_a,C_a \leq 10^9
- 1\leq N \leq 10^{14}
- 1\leq M,L \leq 10^5
- Each of S'_i and T'_i is one of
U,D,L,R. - 1 \leq A_i,B_i \leq 10^9
- A_1+\dots+A_M=B_1+\dots+B_L=N
- All given values are integers.
Input
The input is given from Standard Input in the following format:
R_t C_t R_a C_a N M L S'_1 A_1 \vdots S'_M A_M T'_1 B_1 \vdots T'_L B_L
Output
Print the answer.
Sample Input 1
0 0 4 2 3 2 1 R 2 D 1 U 3
Sample Output 1
1
In this case, S= RRD and T= UUU, and the movements proceed as follows:
- Initially, Takahashi is at cell (0,0) and Aoki is at cell (4,2).
- After the 1st move, Takahashi is at cell (0,1) and Aoki is at cell (3,2).
- After the 2nd move, Takahashi is at cell (0,2) and Aoki is at cell (2,2).
- After the 3rd move, Takahashi is at cell (1,2) and Aoki is at cell (1,2).
Thus, the number of times Takahashi and Aoki are at the same cell immediately after a move is 1.
Sample Input 2
1000000000 1000000000 -1000000000 -1000000000 3000000000 3 3 L 1000000000 U 1000000000 U 1000000000 D 1000000000 R 1000000000 U 1000000000
Sample Output 2
1000000001
From the 2000000000-th move to the 3000000000-th move, Takahashi and Aoki are at the same cell immediately after a move for 1000000001 times.
Sample Input 3
3 3 3 2 1 1 1 L 1 R 1
Sample Output 3
0
Sample Input 4
0 0 0 0 1 1 1 L 1 R 1
Sample Output 4
0