この問題は工夫したシミュレーションにより解くことができます。

まずは次の問題を考えます。

問題(★)「高橋君は \((R_t,C_t)\) から方向 \(D_t\) へ、青木君は \((R_a,C_a)\) から方向 \(D_a\) へ、\(1\) 回の行動で \(1\) マスずつ移動します。\(1\) 回以上行動した後、二人が同じマスいることがあるか判定し、あるなら最小行動回数を求めてください」

この問題の答えは \(D_t=D_a\) のケースに注意しつつ、移動回数 \(X\) に関する連立方程式

\(\begin{cases} R_t+X r'_t=R_a+Xr'_a\\ C_t+Xc'_t=C_a+Xc'_a \end{cases}\)

を解くことで \(O(1)\) で求めることができます。（\(r'_d, c'_d\) は 方向 \(D_d\) に \(1\) 回移動したときのマスの番号の変化を表す）

元の問題に戻ります。青木君と高橋君がそれぞれ一定の方向に移動し続けている間は、問題(★)によりまとめて計算することができます。よって元の問題は \(O(M+L)\) 個の問題(★)を解くことで答えを求めることができ、計算量は \(O(M+L)\) となります。

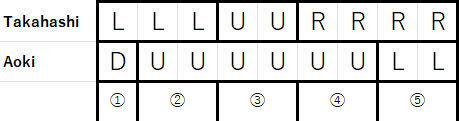
例えば高橋君の移動が LLLUURRRR であり、青木君の移動が DUUUUUULL であるとき、以下のような \(5\) つの区間に分けて考えればよいです。