Rephrasing the problem

Sort \(X\) in ascending order to make \(X_1 \leq X_2 \leq \dots \leq X_N\).

When a base station is placed at coordinate \(r\) with signal strength \(x\), it covers the coordinate range between \(r-\frac{x}{2}\) and \(r + \frac{x}{2}\), inclusive, whose length is \(x\). The indices of the house within form a consecutive integers.

The minimum signal strength \(x\) of a base station that covers house \(l\) through house \(r\) (\(l \leq r\)) is \((X_r - X_l)\).

Thus, the problem is rephrased as follows: split \(1, \dots, N\) into \(M\) subarrays to minimize the sum of \((X_r - X_l)\) for each range.

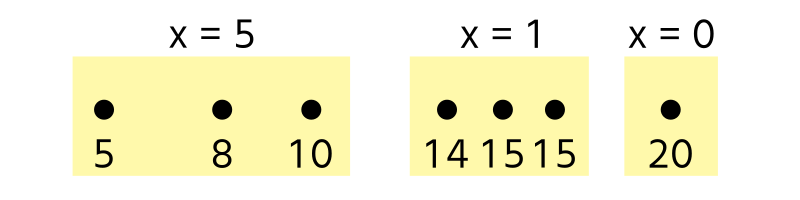
Further rephrasing the problem

Now, let \(D_i := X_{i+1} - X_i\) (\(i = 1,\cdots,N-1\)). This is illustrated as purple numbers in the figure below. Then,

\[(X_r - X_l) = D_l + \dots + D_{r-1},\]

so the problem is equivalent to choosing \((M-1)\) elements among \(D_1, \dots, D_{N-1}\) and remove them to minimize the minimum value of the sum of the remaining.

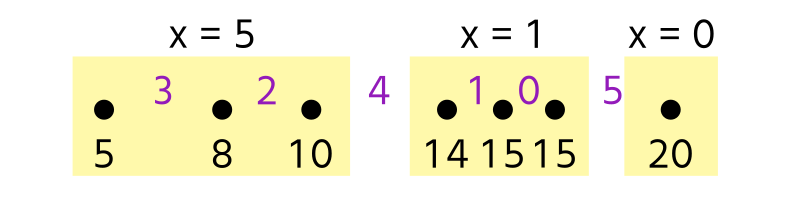
Therefore, the answer can be obtained by sorting \(D\) in ascending order and finding the sum of the first \((N-M)\) elements.

Sample code

Most major languages provide array sorting as a standard library function, which facilitates implementation.

#include <iostream>
#include <cstdio>
#include <string>
#include <vector>
#include <array>
using std::cin;
using std::cout;
using std::cerr;
using std::endl;
using std::string;
using std::pair;
using std::vector;
using std::min;
using std::max;
using std::array;
#include <atcoder/all>

typedef long long int ll;

ll n, m;
vector<ll> x;

void solve () {
	sort(x.begin(), x.end());

	vector<ll> d;
	for (ll i = 0; i < n-1; i++) {
		d.push_back(x[i+1] - x[i]);
	}
	sort(d.begin(), d.end());

	ll ans = 0;
	for (ll i = 0; i < n-m; i++) {
		ans += d[i];
	}

	cout << ans << "\n";
}

int main (void) {
	std::ios_base::sync_with_stdio(false);
	cin.tie(nullptr);
	
	cin >> n >> m;
	x.resize(n);
	for (ll i = 0; i < n; i++) {
		cin >> x[i];
	}

	solve();

	return 0;
}