Regarding one operation as \(K\) steps, consider the following DP (Dynamic Programming):

\(\mathrm{dp}[(u,v)][k]\): the minimum steps required to reach vertex \(v\) from vertex \(u\) as the result of the \(k\)-th step of an operation.

For any vertex \(v\) adjacent to vertex \(v\), one can set \(\mathrm{dp}[(1,v)][1]=1\). (Alternatively, we can define a virtual vertex \(X\) and let \(\mathrm{dp}[(X,1)][K]=0\).) The transitions of the DP is as follows:

• If \(k\neq K\): \(\mathrm{dp}[(v,w)][k+1]\leftarrow \mathrm{dp}[(u,v)][k]+1\) for all vertices \(w\) adjacent to \(v\) (but \(w\neq u\)).

• If \(k=K\): \(\mathrm{dp}[(v,w)][1]\leftarrow \mathrm{dp}[(u,v)][k]+1\) for all vertices \(k\) adjacent to vertex \(v\).

This can be evaluated with BFS (Breadth-First Search), but it will lead to a TLE (Time Limit Exceeded verdict). This is explained by considering the number of times the transition \(\mathrm{dp}[(v,w)][k+1]\leftarrow \mathrm{dp}[(u,v)][k]+1\) occurs: since there are \(d\) possible values for \(u\) and \(w\) (where \(d\) is the degree of \(v\)) and \(K\) values for \(k\), the transition count can accumulate to \(\Theta(N^2K)\) time.

But here is an important observation: for any vertex \(v\), it is sufficient to perform the transition \(\mathrm{dp}[(v,w)][k+1]\leftarrow \mathrm{dp}[(u,v)][k]+1\) at most twice for each \(u\). In other words, it is sufficient to consider the state of reaching vertex \(u\) as the \((k+1)\)-th step at most twice.

This figure explains the reason:

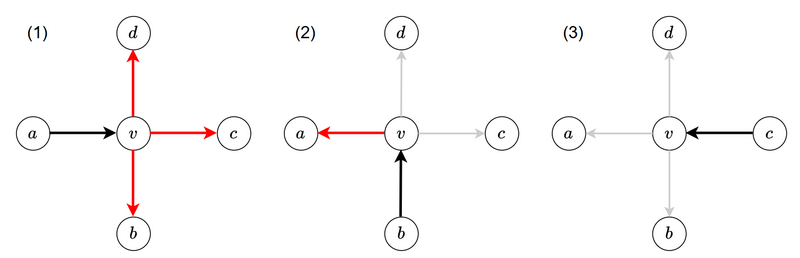
1. When you visit \(v\) from \(b\) for the first time, the following transitions occur: \(v\to b, v\to c\), and \(v\to d\).
2. Next time you visit \(v\) from \(b\), only \(v\to a\) may be updated. Transitions like \(v\to c\) and \(v\to d\) are already processed when \(v\) is visited from \(a\).
3. When you visit \(v\) for the third time, all transitions have been already covered by the first and second, so no new transitions occur.

Hence, we can maintain for each \(k\) how many times \(v\) was visited so far as the \(k\)-th step, and skip the third and subsequence visits. This way, the complexity is bounded by \(O(NK)\).

For implementation, we can regard each edge as bidirectional directed edges, numbering the \(i\)-th edge in the original graph (\(0\)-based index) as \(2i\) and \(2i+1\), in order to avoid using associated arrays.

from collections import deque


def solve():
    N, K = map(int, input().split())
    G = [[] for i in range(N)]
    for i in range(N - 1):
        u, v = map(lambda x: int(x) - 1, input().split())
        G[u].append((v, 2 * i))
        G[v].append((u, 2 * i + 1))

    dp = [[-1] * (2 * N - 2) for i in range(K)]
    ans = [-1] * N
    cnt = [[0] * N for i in range(K)]
    dq = deque([(0, 0, -1)]) # (総歩数，頂点番号，有向辺の番号)
    while dq:
        d, v, e = dq.popleft()
        if d % K == 0 and ans[v] == -1:
            ans[v] = d // K
        if cnt[d % K][v] == 2:
            continue
        cnt[d % K][v] += 1
        for u, e2 in G[v]:
            if e ^ e2 == 1 and d % K != 0:
                continue
            if dp[(d + 1) % K][e2] == -1:
                dp[(d + 1) % K][e2] = d + 1
                dq.append((d + 1, u, e2))

    print(*ans[1:])


for _ in range(int(input())):
    solve()