G - AtCoder Express 4 Editorial
by  toam
toam
この問題はいわゆる 区間に辺を張るテク を用いて解くことができます.このテクニックを用いる典型的な問題として以下の問題があります.
\(N\) 頂点 \(0\) 辺のグラフがある.\(i=1,2,\ldots,M\) 回に対して以下を行う.
- 整数 \(l_i,r_i,L_i,R_i,w_i\) が与えられる.頂点 \(a\ (l_i\leq a\leq r_i)\) から頂点 \(b\ (L_i\leq b\leq R_i)\) へ重み \(w_i\) の辺を追加する.
得られたグラフに対し,頂点 \(s\) から各頂点への最短距離を求めよ.
この問題を問題文通りに解こうとすると,辺の本数が \(O(N^2M)\) 本となってしまいます.ここで,うまくグラフを構成することで辺の本数を減らすというのが区間に辺を張るテクです.
グラフの頂点を拡張して segment tree の区間に対応する頂点を追加することで,辺の本数を減らすことができます.以下の図がわかりやすいので引用します.
(英語解説向け:下図では \([1,4]\) から \([3,7]\) にコスト \(C\) の辺を張る様子を表しています)

(出典:https://x.com/noshi91/status/1193177214453338113 )
このグラフの頂点数は \(O(N+M)\) 個,辺の本数は \(O(N + M \log N)\) 個になるため,最短距離は dijkstra 法で 計算量 \(O(N\log N+M\log^2 N)\) で解くことができます.
区間に辺を張るテクを用いて解ける問題(ネタバレを含みます)
本問題も,同様のグラフを作ることで辺の本数を減らすことができます.
グラフの構築の仕方について考えます.頂点 \(1\) 側を西,頂点 \(N\) 側を東としたとき,まずは東行きの列車の処理を考えます. segment tree の各頂点に対して,乗車する側では「その頂点に対応する区間の 東端 の駅に到達するまでにかかる最小コスト」,降車する側では「その頂点に対応する区間の 西端 の駅に到達するまでにかかる最小コスト」を考えることにします.
グラフの辺は次のようになります.
- 乗車する側
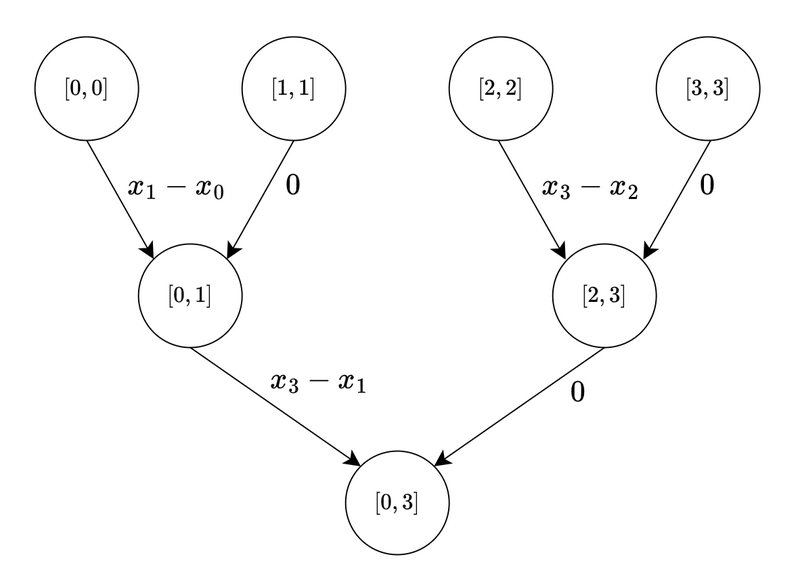
- 降車する側
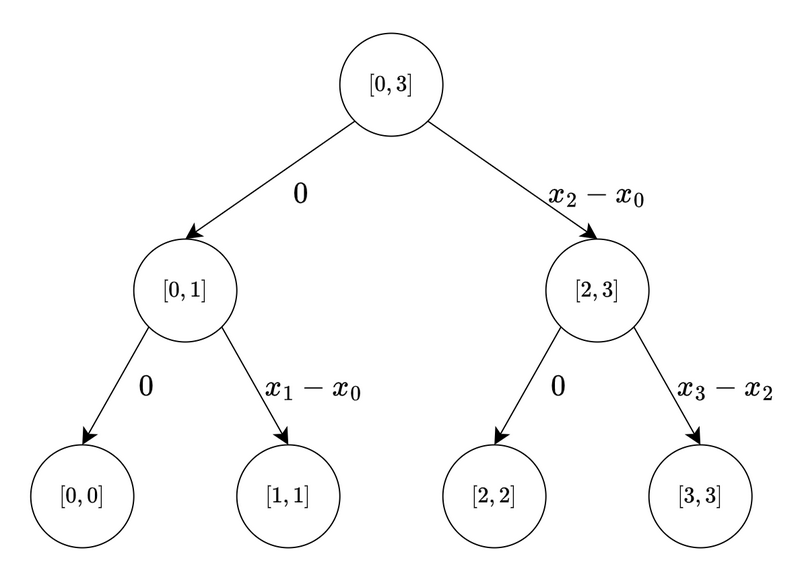
このとき,例えば \((l,r,L,R)=(1,2,4,6)\) であるような列車は以下のようにして表現できます.
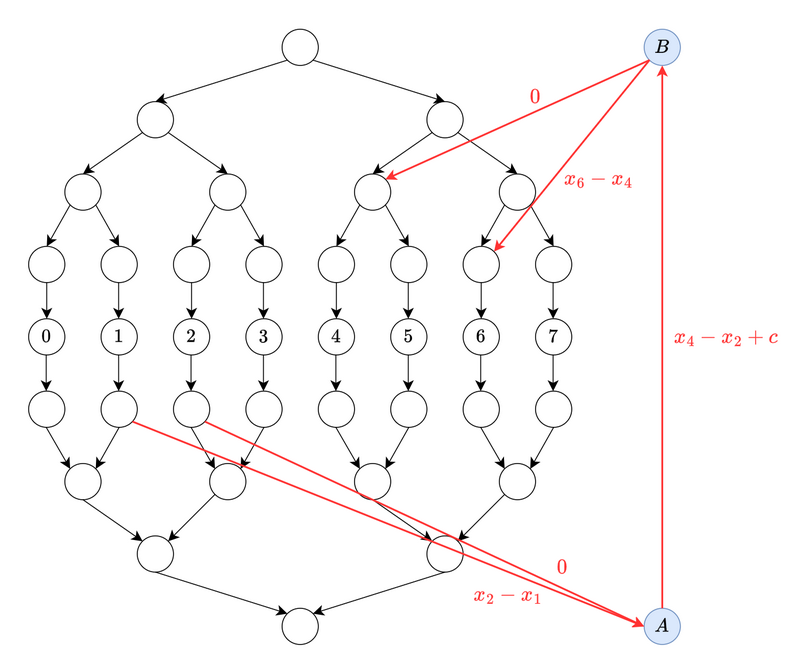
具体的には
- 乗車する側の頂点を集約する頂点 \(A\),降車する側の頂点を集約する頂点 \(B\) を作る.
- 乗車する区間に対応する各頂点に対し,そこから頂点 \(A\) に辺を張る.辺の重みはその頂点が対応する segment tree の区間を \([a,b]\) としたとき,\(x_r-x_b\) である.
- 頂点 \(A\) から頂点 \(B\) に辺を張る.辺の重みは \(x_L-x_r+c\) である.
- 降車する区間に対応する各頂点に対し,頂点 \(B\) からその頂点に辺を張る.辺の重みはその頂点が対応する segment tree の区間を \([a,b]\) としたとき,\(x_a-x_L\) である.
頂点 \(u\ (1\leq u\leq 2)\) から頂点 \(v\ (4\leq v\leq 6)\) に重み \(x_v-x_u+c\) のパスが追加されていることが実際に上の図をたどることで確認できます.
同様にして西行きの列車を管理するグラフを作ることができます.
東行きの列車を管理するグラフと西行きの列車を管理するグラフを連結させることで,頂点 \(0\) からの距離を dijkstra 法で求めることができます.グラフの頂点数は \(O(N+M)\) 個,辺の本数は \(O(N + M \log N)\) 個になるため,計算量は \(O(N\log N+M\log^2 N) \) です.
自明なグラフの縮約をすることで,頂点の個数は \(5N'+M\) にすることができます(\(N'\) は \(N\) 以上の最小の \(2\) べき).
posted:
last update:
