G - Count Cycles 解説 /

実行時間制限: 6 sec / メモリ制限: 1024 MiB

配点 : 600 点

問題文

N 頂点 M 辺の無向グラフ G があります。 G は自己ループを含みませんが、多重辺は含む可能性があります。 頂点には 1 から N までの、辺には 1 から M までの番号がそれぞれ付けられており、辺 i は頂点 U_i,V_i の間に張られています。

G に含まれるサイクルの個数を 998244353 で割った余りを求めてください。

より形式的には、与えられた辺集合の部分集合 \lbrace e_1,e_2,\dots,e_k\rbrace \subseteq \lbrace 1,2,\dots,M\rbrace\ (k\geq 2) であって以下の条件を満たすものの個数を 998244353 で割った余りを求めてください。

  • (e_1,e_2,\dots,e_k) の並び替え (e_1',e_2',\dots,e_k') および頂点列 (v_1,v_2,\dots,v_k) の組であって、以下を全て満たすものが存在する。
    • v_1,v_2,\dots,v_k は互いに相異なる
    • 全ての j\ (1\leq j\leq k) について、辺 e_j' は頂点 v_j,v_{(j\bmod k) + 1} の間に張られている

制約

  • 2\leq N \leq 20
  • 2\leq M \leq 2\times 10^5
  • 1\leq U_i < V_i \leq N
  • 入力は全て整数

入力

入力は以下の形式で標準入力から与えられる。

N M
U_1 V_1
U_2 V_2
\vdots
U_M V_M

出力

答えを出力せよ。

入力例 1

3 4
1 3
1 2
2 3
1 3

出力例 1

3

以下の図の通り、全部で 3 個のサイクルが存在します。 丸の中に書かれた数字と線の横に書かれた数字はそれぞれ頂点番号、辺番号を表します。 赤い線がサイクルに含まれる辺、黒い線がそれ以外の辺を表します。

与えられたグラフを表す図が三つ横一列に並んでいる。左の図では辺 1,2,3 が、中央の図では辺 2,3,4 が、右の図では辺 1,4 がそれぞれ赤く塗られている。

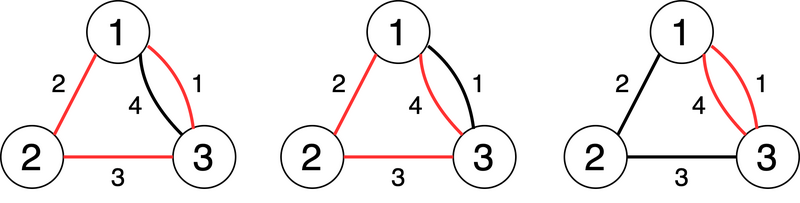
左から順に、辺集合 \lbrace 1,2,3 \rbrace,\lbrace 2,3,4 \rbrace,\lbrace 1,4 \rbrace をそれぞれ選ぶことに対応しています。

入力例 2

4 2
1 4
2 3

出力例 2

0

入力例 3

5 15
1 5
3 4
2 3
2 4
3 5
4 5
2 5
2 3
1 3
4 5
2 5
4 5
1 2
3 4
1 5

出力例 3

166

Score : 600 points

Problem Statement

There is an undirected graph G with N vertices and M edges. G does not contain self-loops, but may contain multi-edges. Vertices are numbered from 1 to N, and edges are numbered from 1 to M, with edge i connecting vertices U_i,V_i.

Find the number, modulo 998244353, of cycles contained in G.

More formally, find the number, modulo 998244353, of subsets \lbrace e_1,e_2,\dots,e_k\rbrace \subseteq \lbrace 1,2,\dots,M\rbrace\ (k\geq 2) of the given edge set that satisfy the following condition.

  • There exists a permutation (e_1',e_2',\dots,e_k') of (e_1,e_2,\dots,e_k) and a vertex sequence (v_1,v_2,\dots,v_k) such that all of the following hold:
    • v_1,v_2,\dots,v_k are pairwise distinct;
    • For all j\ (1\leq j\leq k), edge e_j' connects vertices v_j,v_{(j\bmod k) + 1}.

Constraints

  • 2\leq N \leq 20
  • 2\leq M \leq 2\times 10^5
  • 1\leq U_i < V_i \leq N
  • All input values are integers.

Input

The input is given from Standard Input in the following format:

N M
U_1 V_1
U_2 V_2
\vdots
U_M V_M

Output

Output the answer.

Sample Input 1

3 4
1 3
1 2
2 3
1 3

Sample Output 1

3

As shown in the figure below, there are a total of 3 cycles. The numbers inside the circles and the numbers next to the lines represent vertex numbers and edge numbers, respectively. Red lines represent edges included in cycles, and black lines represent the other edges.

Three figures representing the graphs are arranged from left to right. Painted red are edges 1,2,3, edges 2,3,4, and edges 1,4 from left to right.

From left to right, these correspond to choosing edge sets \lbrace 1,2,3 \rbrace,\lbrace 2,3,4 \rbrace,\lbrace 1,4 \rbrace, respectively.

Sample Input 2

4 2
1 4
2 3

Sample Output 2

0

Sample Input 3

5 15
1 5
3 4
2 3
2 4
3 5
4 5
2 5
2 3
1 3
4 5
2 5
4 5
1 2
3 4
1 5

Sample Output 3

166