 /
/ 
実行時間制限: 4 sec / メモリ制限: 1024 MiB
配点 : 525 点
問題文
N 頂点 M 辺の無向グラフ G_0 が与えられます。 G_0 の頂点および辺は、それぞれ頂点 1, 頂点 2, \ldots, 頂点 N および辺 1, 辺 2, \ldots, 辺 M と番号づけられており、 辺 i (1\leq i\leq M) は頂点 U_i と頂点 V_i を結んでいます。
高橋君はグラフ G と、駒 1, 駒 2, \ldots, 駒 N と番号づけられた N 個の駒を持っています。
最初、G=G_0 であり、さらに G の頂点 i (1\leq i\leq N) には駒 i が置かれています。
高橋君はこれから Q 回の操作を順に行います。 i 回目 (1\leq i\leq Q) の操作では 1 以上 M 以下の整数 X_i が与えられ、次の操作を行います。
G において駒 U_{X_i} と駒 V_{X_i} が異なる頂点に置かれており、 それらの間に( G 上の)辺 e が存在するならばその辺を縮約したグラフ G' を作成する。 この際、自己ループができた場合は取り除き、多重辺が存在した場合は単純辺に置き換える。
その後、G において辺 e が結んでいた 2 頂点に置かれていた駒はすべて、G' の e の縮約によって新たに生成された頂点に置く。 G 上のその他の頂点に置かれていた駒については、G' の対応する頂点に置く。 最後に、このようにしてできた G' を新たな G とする。
駒 U_{X_i} と駒 V_{X_i} が同じ頂点に置かれていた場合、あるいは置かれている頂点の間が辺で結ばれていなかった場合は何も行わない。
i=1,2,\ldots, Q 回目の操作それぞれについて、i 回目の操作の後の G の辺の数を出力してください。
辺の縮約 とは
頂点 u と頂点 v を結ぶ辺の縮約とは、頂点 u,v を 1 つの頂点にまとめる操作です。 より正確には、G に対して辺の縮約を行なって得られるグラフとは G に対して次の操作を行って得られるものを指します。- G に新たに頂点 w を追加する。
- G 上の u,v 以外の各頂点 x について、u と x を結ぶ辺、あるいは v と x を結ぶ辺の少なくとも一方が存在するとき、かつその時に限り、w と x を結ぶ辺を加える。
- 頂点 u,v を削除し、頂点 u と v を結ぶ辺および頂点 u または v と他の頂点を結ぶ辺をすべて削除する。
制約
- 2\leq N\leq 3\times 10^5
- 1\leq M\leq 3\times 10^5
- 1\leq U_i<V_i\leq N
- i\neq j ならば (U_i,V_i)\neq (U_j,V_j)
- 1\leq Q\leq 3\times 10^5
- 1\leq X_i\leq M
- 入力はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
N M U_1 V_1 U_2 V_2 \vdots U_M V_M Q X_1 X_2 \ldots X_Q
出力
Q 行出力せよ。 i 行目 (1\leq i\leq Q) には、i 回目の操作の後の G の辺の数を出力せよ。
入力例 1
7 7 1 2 1 3 2 3 1 4 1 5 2 5 6 7 5 1 2 3 1 5
出力例 1
4 3 3 3 2
最初、G は下図のようになっています。丸付き数字はその番号の駒を表します。
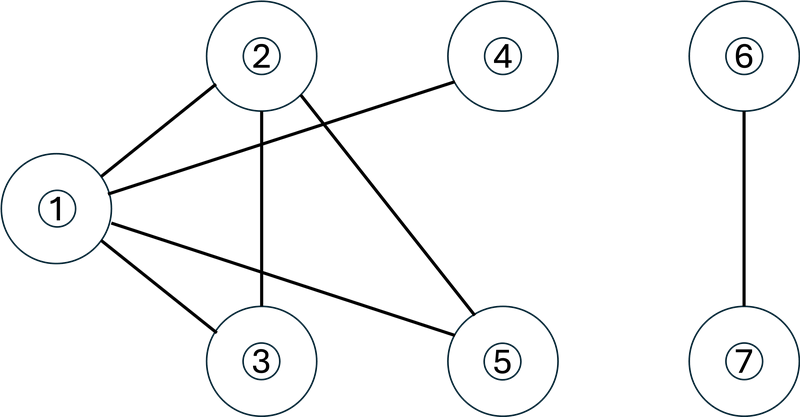
1 回目の操作では、駒 1 と駒 2 が置かれている頂点の間の辺(下図左)の縮約を行います。
操作後、G は下図右のようになり、特に辺の数は 4 です。
自己ループの削除および多重辺の単純辺への置換が行われていることに注意してください。
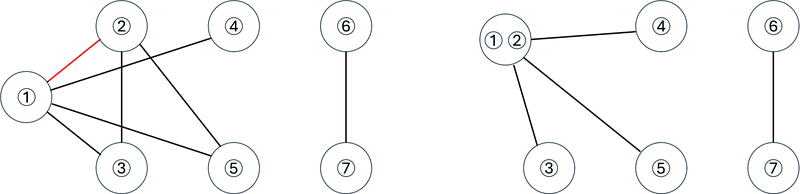
2 回目の操作では、駒 1 と駒 3 が置かれている頂点の間の辺の縮約を行います。
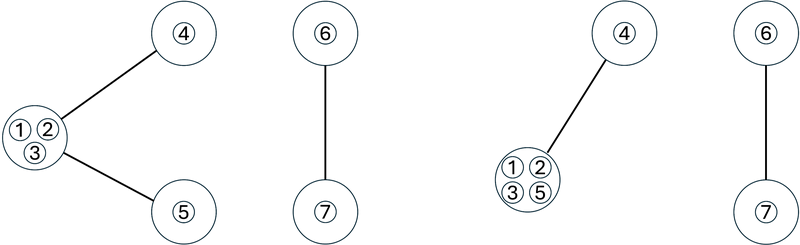
操作後、G は下図左のようになり、辺の数は 3 となります。
3 回目の操作では、駒 2 と駒 3 は同じ頂点に置かれているため、G はそのままであり、辺の数も 3 のままです。
4 回目の操作でも、駒 1 と駒 2 は同じ頂点に置かれているため、G はそのままであり、辺の数も 3 のままです。
5 回目の操作では、駒 1 と駒 5 が置かれている頂点の間の辺の縮約を行います。
操作後、G は下図右のようになり、辺の数は 2 となります。
よって、4,3,3,3,2 をこの順に改行区切りで出力します。
Score : 525 points
Problem Statement
You are given an undirected graph G_0 with N vertices and M edges. The vertices and edges of G_0 are numbered as vertices 1, 2, \ldots, N and edges 1, 2, \ldots, M, respectively, and edge i (1\leq i\leq M) connects vertices U_i and V_i.
Takahashi has a graph G and N pieces numbered as pieces 1, 2, \ldots, N.
Initially, G=G_0, and piece i (1\leq i\leq N) is placed on vertex i of G.
He will now perform Q operations in order. The i-th operation (1\leq i\leq Q) gives an integer X_i between 1 and M, inclusive, and performs the following operation:
In G, if pieces U_{X_i} and V_{X_i} are placed on different vertices and there exists an edge e (on G) between them, create a graph G' by contracting that edge. In this case, if self-loops are created, remove them, and if multi-edges exist, replace them with simple edges.
Then, all pieces that were placed on the two vertices connected by edge e in G are placed on the newly generated vertex by the contraction of e in G'. Pieces that were placed on other vertices in G are placed on the corresponding vertices in G'. Finally, set this resulting G' as the new G.
If pieces U_{X_i} and V_{X_i} are placed on the same vertex, or if the vertices they are placed on are not connected by an edge, do nothing.
For each of the operations i=1,2,\ldots, Q, output the number of edges in G after the i-th operation.
Edge Contraction
Edge contraction of an edge connecting vertices u and v is an operation that merges vertices u,v into one vertex. More precisely, a graph obtained by performing edge contraction on G refers to the result of performing the following operations on G:- Add a new vertex w to G.
- For each vertex x other than u,v in G, if and only if at least one of the edge connecting u and x or the edge connecting v and x exists, add an edge connecting w and x.
- Delete vertices u,v and remove all edges connecting vertices u and v, as well as all edges connecting vertex u or vertex v with other vertices.
Constraints
- 2\leq N\leq 3\times 10^5
- 1\leq M\leq 3\times 10^5
- 1\leq U_i<V_i\leq N
- (U_i,V_i)\neq (U_j,V_j) if i\neq j.
- 1\leq Q\leq 3\times 10^5
- 1\leq X_i\leq M
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N M U_1 V_1 U_2 V_2 \vdots U_M V_M Q X_1 X_2 \ldots X_Q
Output
Output Q lines. On the i-th line (1\leq i\leq Q), output the number of edges in G after the i-th operation.
Sample Input 1
7 7 1 2 1 3 2 3 1 4 1 5 2 5 6 7 5 1 2 3 1 5
Sample Output 1
4 3 3 3 2
Initially, G is as shown in the figure below. The circled numbers represent pieces with those numbers.

In the 1st operation, we contract the edge between the vertices where pieces 1 and 2 are placed (left figure below).
After the operation, G becomes as shown in the right figure below, and in particular, the number of edges is 4.
Note that self-loops have been removed and multi-edges have been replaced with simple edges.

In the 2nd operation, we contract the edge between the vertices where pieces 1 and 3 are placed.
After the operation, G becomes as shown in the left figure below, and the number of edges becomes 3.
In the 3rd operation, since pieces 2 and 3 are placed on the same vertex, G remains unchanged, and the number of edges remains 3.
In the 4th operation as well, since pieces 1 and 2 are placed on the same vertex, G remains unchanged, and the number of edges remains 3.
In the 5th operation, we contract the edge between the vertices where pieces 1 and 5 are placed.
After the operation, G becomes as shown in the right figure below, and the number of edges becomes 2.
Thus, output 4,3,3,3,2 in this order, separated by newlines.
