G - Longest Chord Chain Editorial /

Time Limit: 2 sec / Memory Limit: 1024 MiB

配点 : 575 点

問題文

円周上に 1 から 2N の番号がついた相異なる 2N 個の点があり、点 1 から時計回りに順に点 2、点 3、…、点 2N と並んでいます。

この円の弦が N 個与えられます。i 番目の弦の端点は点 A_i と点 B_i であり、2N 個の値 A_1,\ldots,A_N,B_1,\ldots,B_N は相異なります。

この円に対し以下の操作を一度ずつ順に行います。

  1. 円の N 本の弦のうち、互いに交わらないように弦を好きな個数選び、残りの弦を削除する。
  2. 円に自由に弦を 1 つ追加する。

適切に操作を行ったとき、操作を終えた後の弦同士の交点の個数として考えられる最大値を求めてください。

制約

  • 1 \leq N \leq 2\times 10^5
  • 1 \leq A_i,B_i \leq 2N
  • 2N 個の値 A_1, \ldots, A_N,B_1,\ldots,B_N は相異なる
  • 入力は全て整数である

入力

入力は以下の形式で標準入力から与えられる。

N
A_1 B_1
A_2 B_2
\vdots
A_N B_N

出力

答えを出力せよ。

入力例 1

3
1 5
6 3
4 2

出力例 1

2

最初、円には弦が 3 本あり、図のようになっています。
操作により点 3 と点 6 を結ぶ弦を削除し、新たな弦を追加することで、弦同士の交点の個数は 2 個となります。

図

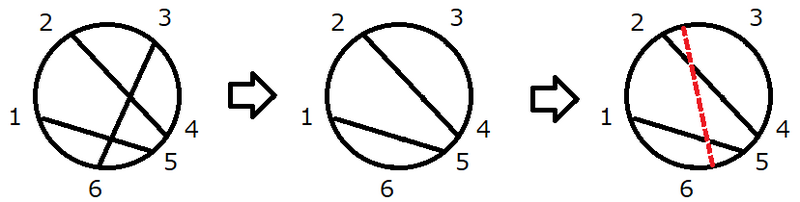
弦同士の交点の個数を 3 個以上にすることはできないため、答えは 2 となります。

最後に追加する弦の端点は、点 1,\ldots, 2N のいずれかである必要はありません。

入力例 2

4
1 8
2 7
3 6
4 5

出力例 2

4

入力例 3

3
1 2
3 4
5 6

出力例 3

2

Score : 575 points

Problem Statement

There are 2N pairwise distinct points, numbered from 1 to 2N, on a circle. Starting from point 1 and going clockwise, the points are arranged as point 2, point 3, ..., point 2N.

You are given N chords on this circle. The endpoints of the i-th chord are points A_i and B_i, and the 2N values A_1,\ldots,A_N,B_1,\ldots,B_N are all distinct.

Perform the following operations on this circle once each in order:

  1. Among the N chords on the circle, choose any number of chords such that no two chosen chords intersect, and delete the remaining chords.
  2. Add one chord freely to the circle.

Find the maximum possible number of intersection points between chords after the operations are completed.

Constraints

  • 1 \leq N \leq 2\times 10^5
  • 1 \leq A_i,B_i \leq 2N
  • The 2N values A_1, \ldots, A_N,B_1,\ldots,B_N are pairwise distinct.
  • All input values are integers.

Input

The input is given from Standard Input in the following format:

N
A_1 B_1
A_2 B_2
\vdots
A_N B_N

Output

Output the answer.

Sample Input 1

3
1 5
6 3
4 2

Sample Output 1

2

Initially, there are 3 chords on the circle, as shown in the figure.
After deleting the chord connecting points 3 and 6 and adding a new chord through the operations, the number of intersection points between chords is 2.

Figure

It is impossible to make the number of intersection points between chords 3 or more, so the answer is 2.

The endpoints of the chord added at the end do not need to be any of the points 1,\ldots, 2N.

Sample Input 2

4
1 8
2 7
3 6
4 5

Sample Output 2

4

Sample Input 3

3
1 2
3 4
5 6

Sample Output 3

2