最初に弦を削除するステップにおいて、他と交わる弦だけでなく、最終的に答えに寄与しない弦も削除することにします。

このとき残る弦は図のようになります。

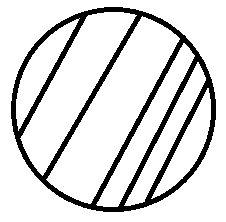
より正確には

残る弦を弦 $1,\ldots,k$ としたとき、$(1,\ldots,k)$ の並び替えである $(i_1,\ldots,i_k)$ と円周上の点 $P$ が存在して、$P$ から時計回りに円周上を辿ったときに「弦 $i_1$ の端点、弦 $i_2$ の端点、……、弦 $i_k$ の端点、弦 $i_k$ の端点、弦 $i_{k-1}$ の端点、……、弦 $i_1$ の端点」がこの順に現れるようにできる。

証明

最後に追加した弦の端点を $P,Q$ とし、$P$ から $Q$ へ至るまでに交わった弦を順に $i_1,\dots,i_k$ とすると条件を満たす。（弦 $1,\ldots,k$ は互いに交わらないため、円弧 $PQ$ と線分 $PQ$ で交わる順序が変わらない）

逆に、残る弦がこの図のようになっているときには、それらの弦全てと交わるように弦を追加することができます。

証明

弦 $i_k$ がなす弧のうち点 $P$ を含まない方から任意に点 $Q$ をとり、$P$, $Q$ を結ぶ弦を追加すれば良い。

円環を切り開き、弦の代わりに区間を考えます。

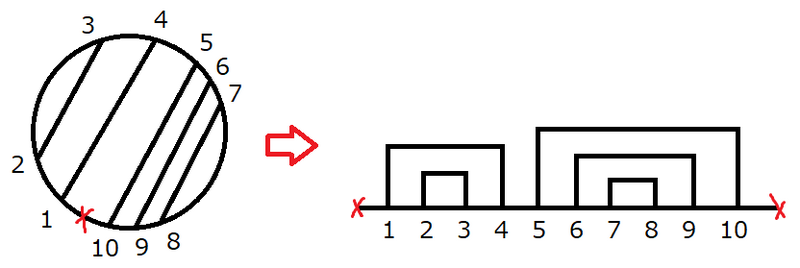
この操作により、元の問題は次の問題に変換されます。

\(N\) 個の区間が与えられる。次のどちらかの条件を満たすようにいくつかの区間 \(I_1,\ldots,I_k\) を選ぶとき、選べる区間の個数の最大値はいくつか？

• \(I_1 \subset\dots\subset I_{k}\)
• ある \(1\leq k' < k\) が存在し、\(I_1 \subset\dots\subset I_{k'}\) かつ \(I_{k'+1}\subset\dots\subset I_k\) かつ \(I_{k'}\cap I_k=\emptyset\)

証明

言い換え後の問題の解が元の問題の解になること：前者のケースでは $I_1$ 内に $P$ を、$I_k$ の外に $Q$ を取れば良い。後者のケースでは $I_1$ 内に $P$ を、$I_{k`+1}$ 内に $Q$ を取れば良い。
元の問題の解が言い換え後の問題の解になること：元の問題の弦と言い換え後の問題の区間を同一視する。円を切り開いた位置を $R$ として、$Q$ を含まない弧 $PR$ 上に端点を持つ弦を、$P$ 側から順に $1,2,\ldots,k'$ 、$P$ を含まない弧 $RQ$ 上に端点を持つ弦を $Q$ 側から順に $k'+1,\ldots,k$ とすればよい。

\(I_1 \subset I_2 \subset\dots\subset I_k\) となっているとき「区間が \(k\) 個入れ子になっている」などのように表現することにします。

以下、与えられる区間 \(I_i=[L_i,R_i]\) は \(R_i\) の昇順にソートされているとします。

前者のケース

\(L_i\) の単調減少部分列の長さの最大値が答えです。セグメントツリーなどを用いることで \(O(N\log N)\) で求めることができます。

証明

一般に $N$ 個の区間 $I_i=[L_i,R_i]$ に対し、 $I_i \subset I_2 \subset \ldots \subset I_k \iff L_k\leq L_{k-1}\leq \ldots \leq L_1 \leq R_1 \leq R_2 \leq \ldots \leq R_k$ が成り立つため。

類題 Typical DP Contest K問題

後者のケース

どの座標で2組に分割するかを全探索します。すなわち、「\(X\) が与えられたとき、\((-\infty,X]\) に含まれる区間の入れ子の最大値と \((X,\infty)\) に含まれる区間の入れ子の最大値」を各 \(X\) について求めます。

\(X\) として考慮すべきものは \(R_i\) のみに限って良いです。

証明

便宜上 \(R_0=-\infty, R_{N+1}=\infty\) とします。\(X\) を任意にとり、\(k\) を \(R_k \leq X < R_{k+1}\) を満たすように取ります。このとき、「\((-\infty,X]\) に含まれる区間」と「\((-\infty,R_k]\) に含まれる区間」は同じであり、「\((X,\infty)\) に含まれる区間」は「\((R_k,\infty)\) に含まれる区間」の部分集合となるため、「\((-\infty,R_k]\) に含まれる区間の入れ子の最大値と \((R_k,\infty)\) に含まれる区間の入れ子の最大値の和」は「\((-\infty,X]\) に含まれる区間の入れ子の最大値と \((X,\infty)\) に含まれる区間の入れ子の最大値の和」以上となります。

前節の最長減少部分列を求める方法としては様々なものが考えられますが、

\(\mathrm{dp}_i[x]=\) \(i\) 番目までのみを考慮したとき、末尾が \(x\) である減少列の長さの最大値

と定めるDPをセグメントツリーによりin-placeに更新するものを考えます。このとき、\((-\infty,R_i]\) に含まれる区間の入れ子の最大値は \(\max_x\mathrm{dp}_i[x]\)、\((R_i,\infty)\) に含まれる区間の入れ子の最大値は \(\max_{x> R_i}\mathrm{dp}_{N}[x]\) として得ることができるため、最長減少部分列を求める過程において追加の \(O(N\log N)\) の計算量でこれらを求めることができます。

以上により、全体で \(O(N\log N)\) でこの問題を解けることがわかりました。

writer解(C++)

#include<bits/stdc++.h>
#include<atcoder/segtree>
using namespace std;

using S=int;
S op(S x,S y){return max(x,y);}
S e(){return 0;}

int main(){
	int n;
	cin >> n;
	vector<array<int,2>>rl;
	for(int i=0;i<n;i++){
		int l,r;
		cin >> l >> r;
		l--,r--;
		if(l>r)swap(l,r);
		rl.push_back({r,l});
	}

	sort(rl.begin(),rl.end());
	atcoder::segtree<S,op,e>seg(2*n);
	
	vector<int>ans(n);
	for(int i=0;i<n;i++){
		auto[r,l]=rl[i];
		ans[i]=seg.prod(l,r)+1;
		seg.set(l,ans[i]);
	}

	for(int i=0;i<n;i++){
		auto[r,l]=rl[i];
		ans[i]+=seg.prod(r,2*n);
	}
	
	cout << *max_element(ans.begin(),ans.end()) << endl;
}