 /
/ 
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 600 点
問題文
H 行 W 列のグリッドがあり、それぞれのマスには 0 または 1 が書かれています。上から i 行目、左から j 行目のマスには整数 A_{i,j} が書かれています。
このグリッドに対して、2 種類の操作を好きな順番で何度でも行うことができます。
- 操作 X: 整数 x\ (1\leq x\leq H) を選ぶ。各整数 1\leq y\leq W に対して A_{x,y} を 1-A_{x,y} で置き換える。
- 操作 Y: 整数 y\ (1\leq y\leq W) を選ぶ。各整数 1\leq x\leq H に対して A_{x,y} を 1-A_{x,y} で置き換える。
操作が終了した後の \displaystyle \sum_{x=1}^H\sum_{y=1}^W A_{x,y} としてあり得る最小値を求めてください。
制約
- 1\leq H\leq 2\times 10^5
- 1\leq W\leq 18
- H,W は整数
- A_{i,1}A_{i,2}\ldots A_{i,W} は
0および1からなる長さ W の文字列
入力
入力は以下の形式で標準入力から与えられる。
H W
A_{1,1}A_{1,2}\ldots A_{1,W}
A_{2,1}A_{2,2}\ldots A_{2,W}
\vdots
A_{H,1}A_{H,2}\ldots A_{H,W}
出力
答えを出力せよ。
入力例 1
3 3 100 010 110
出力例 1
2
以下のように操作すると、グリッドの状態は下図のように変化し \displaystyle \sum_{x=1}^H\sum_{y=1}^W A_{x,y}=2 にすることができます。
- 操作 Y で y=1 を選ぶ
- 操作 X で x=2 を選ぶ
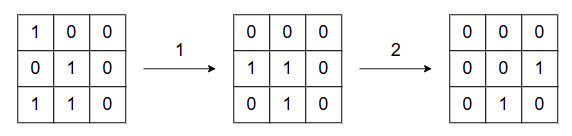
\displaystyle \sum_{x=1}^H\sum_{y=1}^W A_{x,y}\leq 1 にすることはできないので答えは 2 です。
入力例 2
3 4 1111 1111 1111
出力例 2
0
入力例 3
10 5 10000 00111 11000 01000 10110 01110 10101 00100 00100 10001
出力例 3
13
Score : 600 points
Problem Statement
There is a H \times W grid, and each cell contains 0 or 1. The cell at the i-th row from the top and the j-th column from the left contains an integer A_{i,j}.
You can perform the following two operations any number of times in any order:
- Operation X: Choose an integer x (1 \leq x \leq H). For every integer 1 \leq y \leq W, replace A_{x,y} with 1 - A_{x,y}.
- Operation Y: Choose an integer y (1 \leq y \leq W). For every integer 1 \leq x \leq H, replace A_{x,y} with 1 - A_{x,y}.
Find the minimum possible value of \displaystyle \sum_{x=1}^H\sum_{y=1}^W A_{x,y} after the process.
Constraints
- 1 \leq H \leq 2\times 10^5
- 1 \leq W \leq 18
- H and W are integers.
- A_{i,1}A_{i,2}\ldots A_{i,W} is a length-W string consisting of
0and1.
Input
The input is given from Standard Input in the following format:
H W
A_{1,1}A_{1,2}\ldots A_{1,W}
A_{2,1}A_{2,2}\ldots A_{2,W}
\vdots
A_{H,1}A_{H,2}\ldots A_{H,W}
Output
Print the answer.
Sample Input 1
3 3 100 010 110
Sample Output 1
2
By performing the following operations, the grid changes as shown below, and you get \displaystyle \sum_{x=1}^H\sum_{y=1}^W A_{x,y} = 2.
- Operation Y with y=1
- Operation X with x=2

It is impossible to make \displaystyle \sum_{x=1}^H\sum_{y=1}^W A_{x,y} \leq 1, so the answer is 2.
Sample Input 2
3 4 1111 1111 1111
Sample Output 2
0
Sample Input 3
10 5 10000 00111 11000 01000 10110 01110 10101 00100 00100 10001
Sample Output 3
13