この記事では index は 0 始まりとします。

公式解説1 では、 \((i,j,k)\) が \(Q\) に入っているかどうかを判定していますが、 キューへの追加の仕方を工夫することでその処理は省略することができます。

具体的には次の通りです。

1. 優先度付きキュー \(Q\) を用意し， \(Q\) に \((f(0,0,0),0,0,0)\) を追加する。
2. 以下を \(K\) 回繰り返す。
   • \(Q\) の最大値を \((\mathrm{val},i,j,k)\) とする．\(Q\) から \((\mathrm{val},i,j,k)\) を削除し、
     • \(j=0\) かつ \(k=0\) なら \(Q\) に \((f(i+1,j,k),i+1,j,k)\) を追加する
     • \(k=0\) なら \(Q\) に \((f(i,j+1,k),i,j+1,k)\) を追加する
     • \(Q\) に \((f(i,j,k+1),i,j,k+1)\) を追加する

実装例(Python)

from heapq import heappop, heappush

N, K = map(int, input().split())
A = sorted(list(map(int, input().split())), reverse=True)
B = sorted(list(map(int, input().split())), reverse=True)
C = sorted(list(map(int, input().split())), reverse=True)

hq = []


def add(i, j, k):
    if i < N and j < N and k < N:
        heappush(hq, (-(A[i] * B[j] + B[j] * C[k] + C[k] * A[i]), i, j, k))


add(0, 0, 0)
for t in range(K):
    val, i, j, k = heappop(hq)
    if t == K - 1:
        print(-val)
    if j==0 and k==0: add(i + 1, j, k)
    if k==0: add(i, j + 1, k)
    add(i, j, k + 1)

添字が3つあると難しいので、まず2つのバージョンを考えます。

1. 優先度付きキュー \(Q\) を用意し， \(Q\) に \((f(0,0),0,0)\) を追加する。
2. 以下を \(K\) 回繰り返す。
   • \(Q\) の最大値を \((\mathrm{val},i,j)\) とする．\(Q\) から \((\mathrm{val},i,j)\) を削除し、
     • \(j=0\) なら \(Q\) に \((f(i+1,j),i+1,j)\) を追加する
     • \(Q\) に \((f(i,j+1),i,j+1)\) を追加する

このアルゴリズムにおいて、「取り出したもの」から「追加したもの」へ矢印を描いた \((i,j)\) のプロットは下図のようになります。

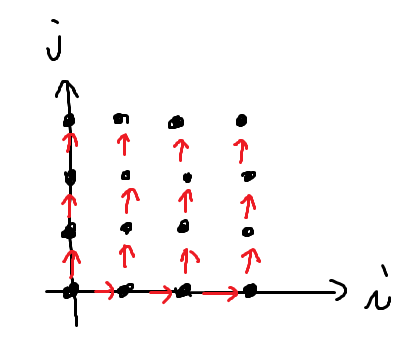
全ての点がちょうど1度指されることから正当性が従います。これを3次元に拡張したものが最初に述べたアルゴリズムになります。

この考え方により、線形篩が線形時間であることを直感的に理解することができます。考えてみましょう。
（整数 \(N\) を \(2^{e_2}\times 3^{e_3}\times 5^{e_5}\times\dots\) により数列 \((e_2,e_3,e_5,\ldots)\) と対応させ、今回のアルゴリズムの無限次元バージョンを考えたものだとみなすことができます）