The answer is the maximum value of “the height at which building \(j\) is not blocked by building \(i\)” for all pairs of buildings \(i<j\). Naively computing this will cost \(\Omega(N^2)\) time, so we consider how to find it fast.

When buildings \(i,j,k\) are in the following relative positions, the only pair that needs to be considered among buildings \((i,j),(i,k),(j,k)\) is \((i,j)\).

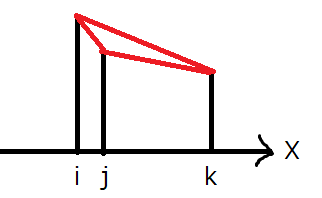
Likewise, buildings \(i,j,k\) are in the following relative positions, the only pair that needs to be considered is \((j,k)\).

Any pair of buildings \((i,k)\) does not need to be considered because one can take an arbitrary building \(j\) in between and apply the discussion for one of the two cases above. Thus, the answer is the maximum value of “the height at which building \(i+1\) is not blocked by building \(i\),” which can be found in a total of \(O(N)\) time.

Beware of precision errors like loss of significance.

Regarding precision errors

When considering only buildings \((i+1)\) and \(i\), building \((i+1)\) is blocked by building \(i\) at the height \(h\) and coordinate \(0\) if and only if \(\displaystyle \frac{h-H_i}{0-X_i}=\frac{H_i-H_{i+1}}{X_i-X_{i+1}}\).
If you try to solve it as \(\displaystyle h=\frac{-(H_i-H_{i+1})X_i}{X_i-X_{i+1}}+H_i\), the addition may result in a large loss of significance.
The error can be reduced by evaluating the numerator and denominator of the form \(\displaystyle h=\frac{H_{i+1}X_i-H_iX_{i+1}}{X_i-X_{i+1}}\), and finally convert them to 64-bit floating point decimals to find the quotient. Especially, if floating-point-number arithmetic operations comply IEE 754, under the constraints of this problem, it can be proved that the resulting floating point decimal resulting from this operation has the same sign as the true value, and the relative error from the true value is at most twice the machine epsilon.
(Brief proof: the absolute value of the denominator is at most around \(2^{32}\), so the true value is preserved even after converted to a 64-bit floating point decimal type. When the absolute value of the numerator is less than \(2^{53}\), its representation in the 64-bit floating point decimal type preserves the true value, so the result of the division preserves the sign, and the relative error is at most the machine epsilon. If the absolute value of the numerator is not less than \(2^{53}\), its representation in the 64-bit floating point decimal type has an error of machine epsilon. Since the absolute value is sufficient large, the result has the same sign as the true value; together with an additional error by the division, the relative error is about twice the machine epsilon.)