全てのビルの組 \(i<j\) についての「ビル \(j\) がビル \(i\) に遮られないような高さ」の最大値が答えになります。これを愚直に計算するには \(\Omega(N^2)\) 時間かかってしまうため、高速に求めることを考えます。

ビル \(i,j,k\) が図のような位置関係にあるとき、\((i,j),(i,k),(j,k)\) の3つのビルの組のうち考慮する必要があるものは \((i,j)\) のみです。

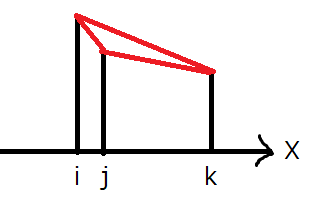
同様に、ビル \(i,j,k\) が下図のような位置関係にあるとき、考慮する必要があるのは\((j,k)\) のみです。

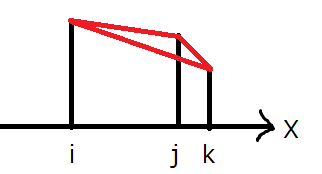
隣り合っていないビルの組 \((i,k)\) は、その間のビル\(j\) を任意に取ると上の 2 つのどちらかの状況が発生するため考慮する必要がありません。よって「ビル \(i+1\) がビル \(i\) に遮られないような高さ」の最大値が答えであり、これは \(O(N)\) 時間で求めることができます。

なお、桁落ちなどの誤差に注意してください。

誤差について

ビル \(i+1\) とビル \(i\) のみを考慮したとき、座標 \(0\) 高さ \(h\) の地点においてビル \(i+1\) がビル \(i\) にギリギリ遮られることは、\(\displaystyle \frac{h-H_i}{0-X_i}=\frac{H_i-H_{i+1}}{X_i-X_{i+1}}\) が成り立つことと同値です。
これを \(\displaystyle h=\frac{-(H_i-H_{i+1})X_i}{X_i-X_{i+1}}+H_i\) などの形で計算すると、加算の際に桁落ちにより大きな誤差が発生する可能性があります。
\(\displaystyle h=\frac{H_{i+1}X_i-H_iX_{i+1}}{X_i-X_{i+1}}\) の形で分子と分母をそれぞれ整数型で計算し、最後に64bit浮動小数点数に変換して除算を行うことで誤差を小さくすることができます。特にIEEE 754に従う浮動小数点数演算において、今回の制約の範囲であれば、この計算により得られる浮動小数点数は、真の値と同じ符号を持ち、真の値との相対誤差は計算機イプシロンの2倍程度に収まることが証明できます。
（略証明：分母の絶対値は \(2^{32}\) 程度であるため、64bit浮動小数点数に変換しても真の値を保つ。分子の絶対値が \(2^{53}\) 未満であるとき、それを64bit浮動小数点数に変換しても真の値を保つので、除算の結果は符号を保ち、高々計算機イプシロンの相対誤差を持つ。特に、真の値が0でないとき、絶対値の最小値は \(\frac{1}{10^9}\) なので、0との比較は正しく行われる。分子の絶対値が \(2^{53}\) 以上であるとき、それを64bit浮動小数点数に変換すると計算機イプシロンの相対誤差を持つ。除算の結果は絶対値が十分大きいため符号は真の値と同じであり、除算により新たに発生する誤差と合わせて、相対誤差は計算機イプシロンの2倍程度となる）