 /
/ 
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 525 点
問題文
H 行 W 列のグリッドがあります。 このグリッドの上から i\ (1\leq i\leq H) 行目、左から j\ (1\leq j\leq W) 列目のマスを (i,j) と表記します。
1 から N までの番号が付けられた N 個の横長のバーがグリッド上に置かれています。 バー i は 1\times 1 のブロックが横に L_i 個繋がった形をしており、その左端のブロックは最初マス (R_i,C_i) 上にあります。 すなわち、バー i は最初マス (R_i,C_i), (R_i,C_i+1), \dots, (R_i,C_i+L_i-1) を占めています。 ここで、相異なる 2 つのバーに占められているマスは存在しないことが保証されます。
現在の時刻は t=0 です。 非負整数 n を用いて t=0.5+n と表されるようなすべての時刻において、i=1,2,\dots,N の順に以下のことが起こります。
- バー i が一番下の行(H 行目)になく、かつバー i が占める各マスの 1 つ下のマスをどのバーも占めていない場合、バー i 全体が 1 マス分下に移動する。 すなわち、その時点でバー i が占めているマスが (r,C_i),(r,C_i+1),\dots,(r,C_i+L_i-1)\ (r < H) であり、どの j\ (0\leq j\leq L_i-1) についてもマス (r+1,C_i+j) を占めているバーが存在しないならば、 バー i の占めるマスが (r+1,C_i),(r+1,C_i+1),\dots,(r+1,C_i+L_i-1) に変化する。
- そうでないならば、何も起こらない。
t=10^{100} においてバー i が占めているマスを (R'_i,C_i), (R'_i,C_i+1), \dots, (R'_i,C_i+L_i-1) とします。 R'_1,R'_2,\dots,R'_N を求めてください。
制約
- 1\leq H,W \leq 2\times 10^5
- 1\leq N \leq 2\times 10^5
- 1\leq R_i\leq H
- 1\leq C_i\leq W
- 1\leq L_i\leq W-C_i+1
- 与えられる初期状態において、相異なる 2 つのバーに占められているマスは存在しない
- 入力は全て整数
入力
入力は以下の形式で標準入力から与えられる。
H W N R_1 C_1 L_1 R_2 C_2 L_2 \vdots R_N C_N L_N
出力
N 行出力せよ。 i\ (1\leq i \leq N) 行目には、R'_i を出力せよ。
入力例 1
4 4 4 1 2 3 3 2 2 2 1 2 2 4 1
出力例 1
2 4 3 4
以下の 3 つの図は左から順に t=0,1,2 でのグリッドの様子を表しています。 色の塗られた長方形は各バーを表し、長方形の中に書かれた数字はそのバーの番号です。
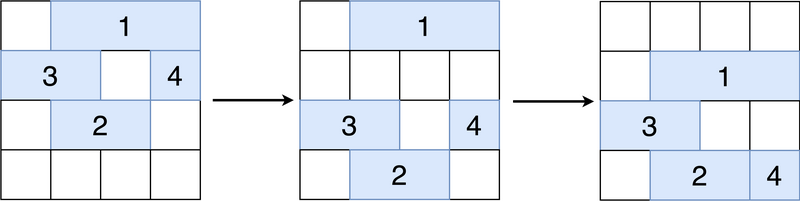
グリッドの状態の変化は以下の通り説明されます。
- t=0.5:
- i=1: バー 1 が占める各マスの 1 つ下のマスである (2,2),(2,3),(2,4) のうち、(2,2) がバー 3 に、(2,4) がバー 4 にそれぞれ占められているため、何も起こらない。
- i=2: バー 2 が占める各マスの 1 つ下のマスである (4,2),(4,3) がいずれも他のバーに占められていないため、バー 2 全体が 1 マス分下に移動する。
- i=3: バー 3 が占める各マスの 1 つ下のマスである (3,1),(3,2) がいずれも他のバーに占められていないため、バー 3 全体が 1 マス分下に移動する。
- i=4: バー 4 が占めるマスの 1 つ下のマスである (3,4) が他のバーに占められていないため、バー 4 全体が 1 マス分下に移動する。
- t=1.5:
- i=1: バー 1 が占める各マスの 1 つ下のマスである (2,2),(2,3),(2,4) がいずれも他のバーに占められていないため、バー 1 全体が 1 マス分下に移動する。
- i=2: バー 2 は一番下の行にあるため、何も起こらない。
- i=3: バー 3 が占める各マスの 1 つ下のマスである (4,1),(4,2) のうち、(4,2) がバー 2 に占められているため、何も起こらない。
- i=4: バー 4 が占めるマスの 1 つ下のマスである (4,4) が他のバーに占められていないため、バー 4 全体が 1 マス分下に移動する。
t=2.5,3.5,\dots においては 1 つ下のマスがすべて空いているようなバーが存在せず、何も起こらないため、t=10^{100} でのグリッドの状態は t=2 でのグリッドの状態(上図における一番右の状態)と同じです。
よって、R'_1=2,R'_2=4,R'_3=3,R'_4=4 です。
入力例 2
382 382 3 3 3 3 8 8 8 2 2 2
出力例 2
382 382 381
入力例 3
5 10 8 2 2 1 4 3 1 4 8 2 1 2 2 2 5 3 5 4 3 4 5 2 1 5 2
出力例 3
5 5 5 4 3 5 4 2
Score: 525 points
Problem Statement
There is a grid with H rows and W columns. Let (i,j) denote the cell at the i-th row from the top and the j-th column from the left.
There are N horizontal bars numbered from 1 to N placed on the grid. Bar i consists of L_i blocks of size 1 \times 1 connected horizontally, and its leftmost block is initially at cell (R_i, C_i). That is, initially, bar i occupies the cells (R_i, C_i), (R_i, C_i + 1), \dots, (R_i, C_i + L_i - 1). It is guaranteed that there is no cell occupied by two different bars.
The current time is t = 0. At every time t = 0.5 + n for some non-negative integer n, the following occurs in order of i = 1, 2, \dots, N:
- If bar i is not on the bottom row (the H-th row), and none of the cells directly below the cells occupied by bar i is occupied by any bar, then bar i moves down by one cell. That is, if at that time bar i occupies the cells (r,C_i),(r,C_i+1),\dots,(r,C_i+L_i-1)\ (r < H), and the cell (r + 1, C_i + j) is not occupied by any bar for all j (0 \leq j \leq L_i - 1), then bar i now occupies (r + 1, C_i), (r + 1, C_i + 1), \dots, (r + 1, C_i + L_i - 1).
- Otherwise, nothing happens.
Let (R'_i, C_i), (R'_i, C_i + 1), \dots, (R'_i, C_i + L_i - 1) be the cells occupied by bar i at time t = 10^{100}. Find R'_1, R'_2, \dots, R'_N.
Constraints
- 1 \leq H, W \leq 2 \times 10^5
- 1 \leq N \leq 2 \times 10^5
- 1 \leq R_i \leq H
- 1 \leq C_i \leq W
- 1 \leq L_i \leq W - C_i + 1
- In the initial state, there is no cell occupied by two different bars.
- All input values are integers.
Input
The input is given from Standard Input in the following format:
H W N R_1 C_1 L_1 R_2 C_2 L_2 \vdots R_N C_N L_N
Output
Print N lines. The i-th line (1 \leq i \leq N) should contain R'_i.
Sample Input 1
4 4 4 1 2 3 3 2 2 2 1 2 2 4 1
Sample Output 1
2 4 3 4
The following three diagrams represent the grid at times t = 0, 1, and 2 from left to right. Colored rectangles represent the bars, and the number inside each rectangle indicates its bar number.

The changes in the grid state are explained as follows:
- At t = 0.5:
- i = 1: The cells directly below bar 1 are (2,2),(2,3),(2,4). Among these, (2,2) is occupied by bar 3 and (2,4) is occupied by bar 4, so nothing happens.
- i = 2: The cells directly below bar 2 are (4,2),(4,3), which are not occupied by any other bar, so bar 2 moves down by one cell.
- i = 3: The cells directly below bar 3 are (3,1),(3,2), which are not occupied by any other bar, so bar 3 moves down by one cell.
- i = 4: The cell directly below bar 4 is (3,4), which is not occupied by any other bar, so bar 4 moves down by one cell.
- At t = 1.5:
- i = 1: The cells directly below bar 1 are (2,2),(2,3),(2,4), which are not occupied by any other bar, so bar 1 moves down by one cell.
- i = 2: Bar 2 is on the bottom row, so nothing happens.
- i = 3: The cells directly below bar 3 are (4,1),(4,2). Among these, (4,2) is occupied by bar 2, so nothing happens.
- i = 4: The cell directly below bar 4 is (4,4), which is not occupied by any other bar, so bar 4 moves down by one cell.
At times t = 2.5, 3.5, \dots, there is no bar such that the cells directly below it are all unoccupied, so nothing happens. Thus, the grid at time t = 10^{100} is the same as at t = 2 (the rightmost diagram above).
Therefore, R'_1 = 2, R'_2 = 4, R'_3 = 3, R'_4 = 4.
Sample Input 2
382 382 3 3 3 3 8 8 8 2 2 2
Sample Output 2
382 382 381
Sample Input 3
5 10 8 2 2 1 4 3 1 4 8 2 1 2 2 2 5 3 5 4 3 4 5 2 1 5 2
Sample Output 3
5 5 5 4 3 5 4 2