視覚的にわかる解説のつもりです。

\(3\leq K\)

隣接しているタイルが \(K + 3\) 個であるようなタイルを外側のタイルとします。 逆に、そうでないタイルを内側のタイルとします。

色分けすると以下のようになります。

これを見るとわかることですが、内側のタイルは、外側のタイルに囲まれています。よって、スタート地点とゴール地点が同じ正方形内にないとき、必ず外側のタイルを \(1\) 度以上通ります。

スタート地点から見て初めに通る外側のタイルは \(4\) 通りです。ゴール地点から見ても同じです。よって、この \(16\) 通りを全探索することを考えます。欲しいのは、外側のタイルから外側のタイルへの最短距離です。

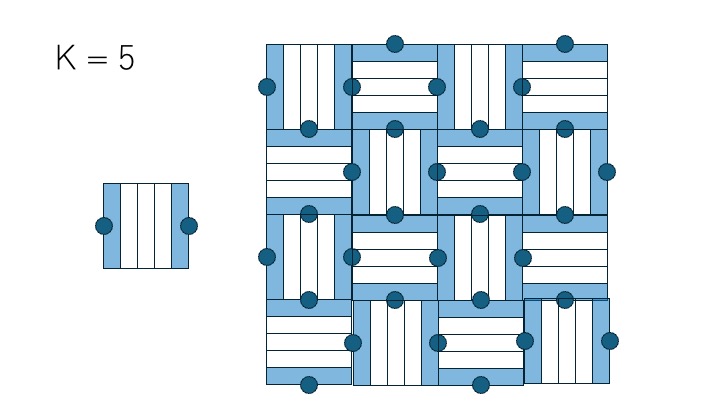
外側のタイルを頂点と見て、頂点を追加したものが上の図です。この頂点間を \(1\) ステップで移動できる組に辺を張ってみるとどのようになるでしょうか

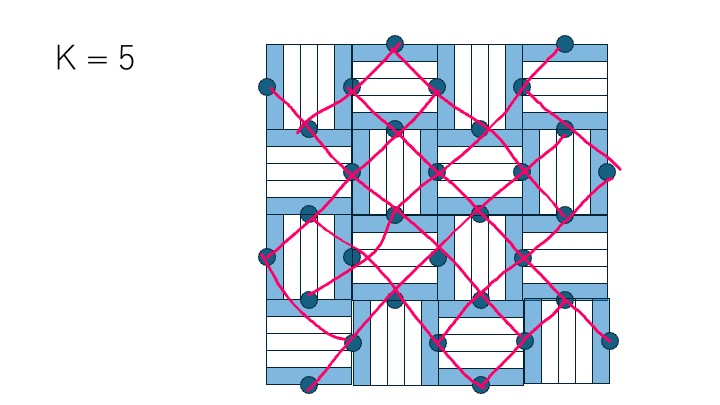
ご覧のように格子を 45 度回転させたものになります。

よって、座標を適当に割り当てて、グリッド上の最短距離問題を解くことで、答えを求めることができます。

ちなみにこれらの辺を以外を辿ったとしても、最短距離は変わりません。なぜなら、外側->内側->外側で行ける外側のタイルは、外側のタイルのみを辿って \(2\) 手以内で行けるからです。

\(K = 2\)

全てのタイルが外側のタイルです。先ほどと同じように頂点として見て、辺を張ってみましょう。グリッドになると嬉しいな

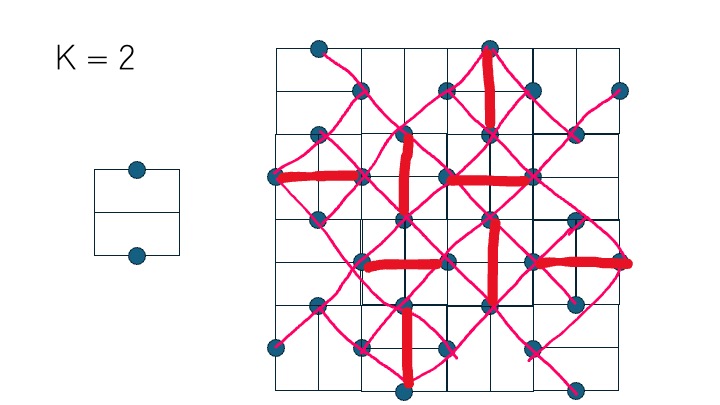
なんだかよくわからない線が追加されています。 このままだとよくわからないので、タイルを外し、45 度回転させてグリッドだけ残したいと思います。

(上の図は縦横の線が 8 本しかないですが、それぞれの正方形に対して 1 本ずつあるので、本当は 16 本あります。グリッドの中身だけ書いて満足してしまいました。)

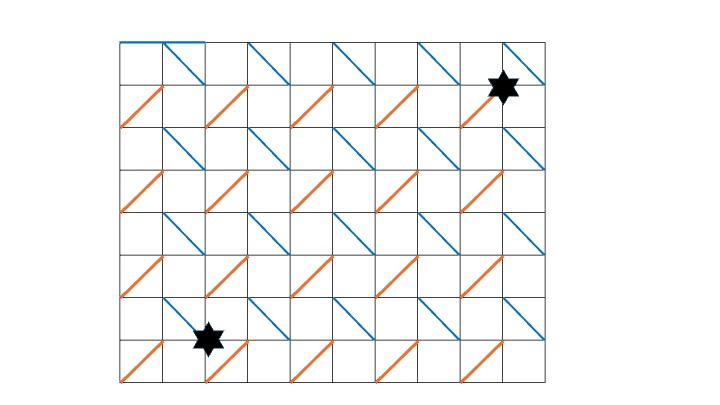
\(3\leq K\) の頃からあった辺はグリッドで、追加された辺が斜めの色付きの線です。

タイルからタイルへの移動にかかるステップ数は、例えばこの星から星への最短距離を求めるような問題に帰着できます。

これは普通に通ると \(15\) ですが、オレンジ色の斜めの線を \(3\) 回通れるので、\(15-3=12\) です。この斜めの線を通る回数は、星から星を対角線とする長方形に含まれるオレンジ色の斜めの線の数が \(3\times 4\) であることから \(3\) であることがわかります。つまり、縦横の短い方を見て、偶奇を考えれば求まります。

逆に、星の位置関係が左上右下である場合は、その向きの青い斜めの線の数を数えれば良いです。

以上の考察を実装すれば良いです。

45 度回転させて座標変換するところが特にバグりやすいと思うので注意してください。

c++ 実装例 7ms