 /
/ 
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 575 点
問題文
二次元座標平面上にタイルが敷き詰められています。
各タイルの形は長方形であり、0 \leq k < K を満たす各整数組 (i, j, k) に対して以下のような規則で対応するタイルが配置されています。
-
i と j の偶奇が一致しているとき、(i, j, k) に対応するタイルは iK \leq x \leq (i + 1)K かつ jK + k \leq y \leq jK + k + 1 なる範囲の (x, y) を覆う。
-
i と j の偶奇が一致していないとき、(i, j, k) に対応するタイルは iK + k \leq x \leq iK + k + 1 かつ jK \leq y \leq (j + 1)K なる範囲の (x, y) を覆う。
2 つのタイルが隣接していることを 2 つのタイルの辺が正の長さの共通部分を持つことにより定義します。
(S_x + 0.5, S_y + 0.5) を含むタイルから隣接しているタイルに移動することを繰り返して (T_x + 0.5, T_y + 0.5) を含むタイルに移動するとき、隣接するタイルに移動する回数の最小値を求めてください。
T 個のテストケースが与えられるので、それぞれについて答えを求めてください。
制約
- 1 \leq T \leq 10^4
- 2 \leq K \leq 10^{16}
- -10^{16} \leq S_x, S_y, T_x, T_y \leq 10^{16}
- 入力される値はすべて整数
入力
入力は以下の形式で標準入力から与えられる。
T
\text{case}_1
\vdots
\text{case}_T
各ケースは以下の形式で与えられる。
K S_x S_y T_x T_y
出力
T 行出力せよ。i 行目には i 番目のテストケースに対する答えを出力せよ。
入力例 1
3 3 -2 1 4 -1 4 8 8 0 2 5 -1000000000000 -1000000000000 1000000000000 1000000000000
出力例 1
4 4 800000000000
1 番目のテストケースについて説明します。
整数組 (i, j, k) に対応するタイルを単にタイル (i, j, k) と表記します。
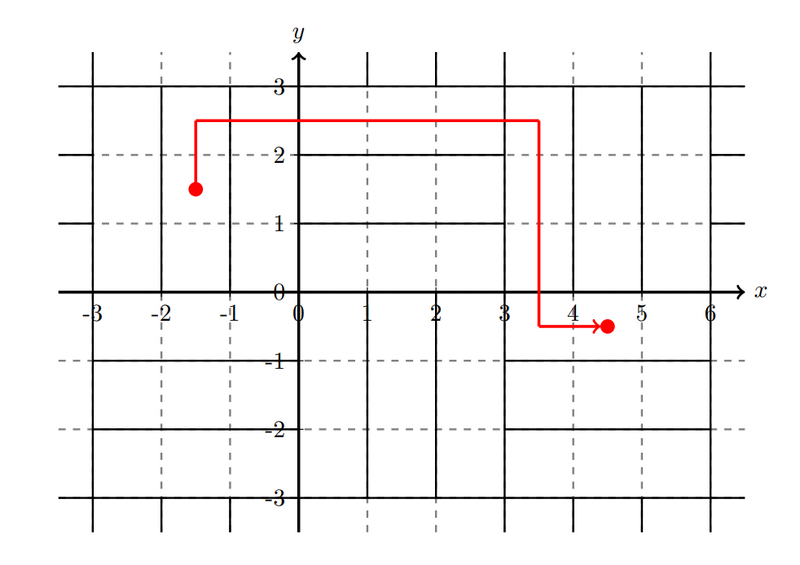
(-1.5, 1.5) はタイル (-1, 0, 1) に含まれ、(4.5, -0.5) はタイル (1, -1, 2) に含まれます。
例えば、タイル (-1, 0, 1) \to (-1, 0, 2) \to (0, 0, 2) \to (1, 0, 0) \to (1, -1, 2) という移動をすることによって、4 回の隣接するタイルへの移動でタイル (1, -1, 2) に辿り着くことができます。
Score: 575 points
Problem Statement
Tiles are laid out covering the two-dimensional coordinate plane.
Each tile is a rectangle, and for each integer triple (i, j, k) satisfying 0 \leq k < K, a corresponding tile is placed according to the following rules:
- When i and j have the same parity (both even or both odd), the tile corresponding to (i, j, k) covers the area where iK \leq x \leq (i + 1)K and jK + k \leq y \leq jK + k + 1.
- When i and j have different parity, the tile corresponding to (i, j, k) covers the area where iK + k \leq x \leq iK + k + 1 and jK \leq y \leq (j + 1)K.
Two tiles are adjacent when their edges have a common segment of positive length.
Starting from the tile containing the point (S_x + 0.5, S_y + 0.5), find the minimum number of times you need to move to an adjacent tile to reach the tile containing the point (T_x + 0.5, T_y + 0.5).
There are T test cases; solve each of them.
Constraints
- 1 \leq T \leq 10^4
- 2 \leq K \leq 10^{16}
- -10^{16} \leq S_x, S_y, T_x, T_y \leq 10^{16}
- All input values are integers.
Input
The input is given from Standard Input in the following format:
T
\text{case}_1
\vdots
\text{case}_T
Each case is given in the following format:
K S_x S_y T_x T_y
Output
Print T lines. The i-th line should contain the answer for the i-th test case.
Sample Input 1
3 3 -2 1 4 -1 4 8 8 0 2 5 -1000000000000 -1000000000000 1000000000000 1000000000000
Sample Output 1
4 4 800000000000
Let us explain the first test case.
Let (i, j, k) denote the tile corresponding to integer triple (i, j, k).
(-1.5, 1.5) is contained in tile (-1, 0, 1), and (4.5, -0.5) is contained in tile (1, -1, 2).
For example, by moving from tile (-1, 0, 1) to (-1, 0, 2) to (0, 0, 2) to (1, 0, 0) to (1, -1, 2), you can reach tile (1, -1, 2) in four moves to an adjacent tile.
