We will consider a grid instead of a coordinate plane. We call those cells reachable to \((-1,-1)\) “inside,” and unreachable “outside.”

We first consider the case where the stones are connected in eight directions.
By enumerating eight cells around each cell beforehand, one can easily determine if these cells are inside or outside easily with BFS (Breadth First Search) etc. (Among the enumerated cells, the top-left cell is always outside; by performing BFS from this cell in four directions, one can reach all cells outside.)

Example: black cells represent lattice points with stones.

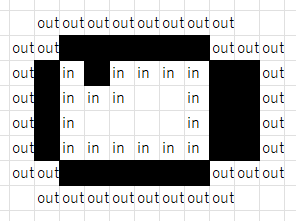
Then, inspect each row. If there is a segment with “outside stone inside … inside stone outside,” then that segment can be counted as “inside” in order to count “inside” points. Beware of cases with consecutive stones, or stones are between inside cells (as in the third row above).

Now we consider disconnected cases. It may seem we can consider each connected component independently, but note that there may be nested structure.
After performing BFS for each connected component and determine whether each cell is outside or inside, when scanning the entire row, there may be part like “outside stone inside …… outside stone inside …… inside stone outside …… inside stone outside,” where some cells inside are labeled outside.

For example, the center row in the following figure does:

Every time you encounter “outside, one or more stones, inside”, the nest increases by one; for “inside, one or more stones, outside”, it decreases by one. By using this fact to manage how many times the current position is surrounded, one can handle this issue.

Also, if there are different connected components sufficiently close to each other, the label (outside / inside) might be overwritten. This can be avoided by defining that stones are connected if the Chebyshev distance is two or less, instead of being eight-adjacent.