まず、高橋くんの泳ぎ方が以下の \(2\) 種類しかなかった場合を考えてみましょう。

• \(1\) 秒あたり体力を \(A_1\) 消費して \(B_1\) [m] 進む
• \(1\) 秒あたり体力を \(A_2\) 消費して \(B_2\) [m] 進む

このとき、高橋くんはこれらを組み合わせることで次のような泳ぎ方をすることができます。

• \(1\) 秒あたり体力を \(tA_1+(1-t)A_2\) 消費して \(tB_1+(1-t)B_2\) [m] 進む

つまり、 \(B\) を \(x\) 軸、 \(A\) を \(y\) 軸に対応させて \((B_1,A_1), (B_2,A_2)\) にプロットすると、これらを結ぶ直線上の任意の点に対応する泳ぎ方ができることになります。

では、点の数を増やしてみるとどうなるでしょうか？

実は、高橋くんが \(N\) 点 \((B_i,A_i)\) に対応する泳ぎ方をすることができるとき、高橋くんはこれら \(N\) 点の凸包の内部または周上の任意の点に対応する泳ぎ方をすることができ、これ以外の泳ぎ方をすることはできません。

略証: まず、直線の場合の議論より凸包の周上の任意の点が作れることがわかります。凸包の内部の任意の点も、凸包の周上の2点を選んでそれらを結ぶ直線で凸包の内部を塗りつぶすように構成できます。
逆に、もし凸包の外部の点が作れたとすると、最初から凸包の外部に点が存在することになってしまい矛盾します。

泳ぎ方を \(xy\) 平面上にプロットして考察を続けます。

• \(x\) 座標が最も大きい ( \(B_i\) が最も大きい) 点を 時間効率が最も良い点 と呼ぶことにします。常にその点に対応する泳ぎ方ができる (そのようにしても体力が持つ) ならば、そうするのが最適です。
• \(A_i / B_i\) が最も小さい点を 体力効率が最も良い点 と呼ぶことにします。常にその点に対応する泳ぎ方をしても \(D_i\) [m] 泳ぎ切ることができないならば、どのようにしても \(D_i\) [m] 泳ぐことはできないので答えは -1 です。

例えば、サンプルでは、時間効率が最も良い点 \(P_\omega\) は \((B,A) = (4,4)\) 、体力効率が最も良い点 \(P_\alpha\) は \((B,A)=(2,1)\) です。

以降、体力効率が最も良い点で \(D_i\) [m] 泳ぎ切ることができ、時間効率が最も良い点では \(D_i\) [m] 泳ぎ切れないものとします。

この状況の下で、体力 \(C_i\) 以内で \(D_i\) [m] を泳ぎ切らなければなりません。この情報を \(xy\) 平面に書き加えましょう。
具体的には、 \((0,0),(D_i,C_i)\) を通る線を書き込みます。この直線上またはそれより下側にある点であれば、どの点に対応する泳ぎ方をしても体力 \(C_i\) 以下で \(D_i\) [m] を泳ぐことができます。逆に、この直線より上側にあるどの点に対応する泳ぎ方をしても \(D_i\) [m] を泳ぎ切ることはできません。

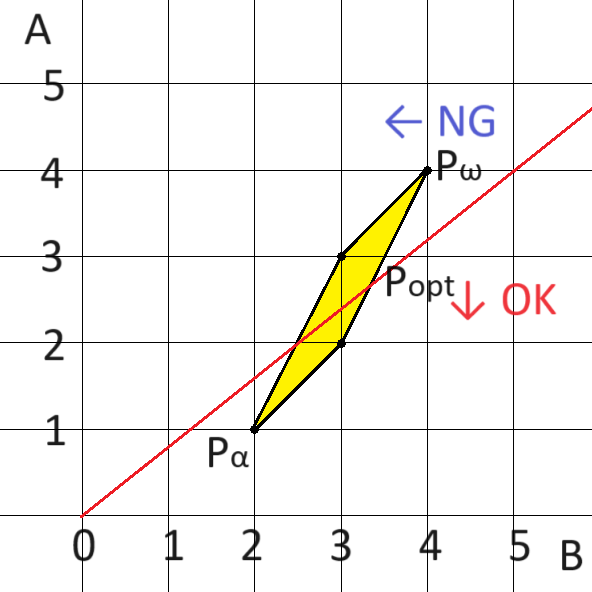
このもとで、求めるべきは \(D_i\) [m] を泳ぎ切れる中で最も秒速が速い (図中では最も右にある) 点です。そして、そのような点は凸包の外周と直線との交点のうち \(x\) 座標が最大のものです。

(下図はサンプルの \(5\) 個目のクエリを図示したものです)

実際にそのような点を (考察を最小限にして) 求めたいならば、 凸多角形と直線の交点を求めるライブラリ が役立ちます。
今回は少し考察して実装を軽くする方法を示します。

体力効率が最も良い点 \(P_\alpha\) で泳ぎ切れて時間効率が最も良い点 \(P_\omega\) では泳ぎ切れないことを利用して、凸包のうち \(P_\alpha\) から \(P_\omega\) を反時計回りに回ることを考えます。
このとき、 \(P_\alpha\) から交点 \(P_{opt}\) までは泳ぎ切れて、 \(P_{opt}\) から \(P_\omega\) までは泳ぎ切れないという状態になります。
よって、まず \(P_{opt}\) が凸包上のどの直線上にあるかを二分探索し、その後 \(P_{opt}\) が当該の直線上のどこにあるかを二分探索すると \(P_{opt}\) の場所を求めることができます。

実装例 (C++):

#include<bits/stdc++.h>

using namespace std;
using pl=pair<long long,long long>;

long long crs(pl a,pl b){
  return a.first*b.second-a.second*b.first;
}
pl sub(pl a,pl b){
  return {a.first-b.first,a.second-b.second};
}
bool plcomp(pl a,pl b){
  return (a.first*b.second < b.first*a.second);
}

int main(){
  long long n;
  cin >> n;
  set<pl> st;
  for(long long i=0;i<n;i++){
    pl ca;
    cin >> ca.second >> ca.first;
    st.insert(ca);
  }
  n=st.size();
  vector<pl> a;
  for(auto &nx : st){a.push_back(nx);}

  // convex hull
  // ref. https://github.com/E869120/kyopro_educational_90/blob/main/sol/041-03.cpp

  if(n>=3){
    vector<pl> g1,g2;
    g1.push_back(a[0]);
    g1.push_back(a[1]);
    g2.push_back(a[0]);
    g2.push_back(a[1]);
    for(long long i=2;i<n;i++){
      while(g1.size()>=2 && crs(sub(g1[g1.size()-1],g1[g1.size()-2]),sub(a[i],g1[g1.size()-1]))<=0){g1.pop_back();}
      while(g2.size()>=2 && crs(sub(g2[g2.size()-1],g2[g2.size()-2]),sub(a[i],g2[g2.size()-1]))>=0){g2.pop_back();}
      g1.push_back(a[i]);
      g2.push_back(a[i]);
    }
    a.clear();
    for(long long i=0;i<g1.size();i++){a.push_back(g1[i]);}
    for(long long i=(long long)g2.size()-2;i>=1;i--){a.push_back(g2[i]);}
  }

  n=a.size();

  long long omega=0,alpha=0;
  for(long long i=0;i<n;i++){
    if(a[omega].first<a[i].first){
      omega=i;
    }
    if(plcomp(a[alpha],a[i])){
      alpha=i;
    }
  }

  long long q;
  cin >> q;

  while(q>0){
    q--;
    long long pow,dist;
    cin >> pow >> dist;

    // if(pow/a[alpha].second*a[alpha].first<dist){}
    if(pow*a[alpha].first<dist*a[alpha].second){
      cout << "-1\n";
      continue;
    }

    // if(pow/a[omega].second*a[omega].first>=dist){}
    if(pow*a[omega].first>=dist*a[omega].second){
      double cres=dist;
      cres/=a[omega].first;
      cout << fixed << setprecision(12) << cres << "\n";
      continue;
    }

    long long p1,p2;

    {
      long long lef=alpha;
      long long rig=omega;
      if(lef>rig){rig+=n;}

      while(lef<=rig){
        long long te=(lef+rig)/2;
        long long i=te%n;

        if(pow*a[i].first>=dist*a[i].second){lef=te+1;}
        else{rig=te-1;}
      }

      p1=(rig%n);
      p2=(lef%n);
    }

    double rv=((double)dist)/((double)a[p1].first);
    double lef=0.0,rig=1.0;

    for(long long tr=0;lef<=rig && tr<100;tr++){
      double te=(lef+rig)/2.0;
      double fir=(1.0-te)*((double)a[p1].first)+te*((double)a[p2].first);
      double sec=(1.0-te)*((double)a[p1].second)+te*((double)a[p2].second);

      if(((double)pow)*fir>=((double)dist)*sec){
        rv=min(rv,((double)dist)/((double)fir));
        lef=te;
      }
      else{
        rig=te;
      }
    }

    cout << fixed << setprecision(12) << rv << "\n";
  }
  return 0;
}