C - Remembering the Days Editorial /

Time Limit: 2 sec / Memory Limit: 1024 MB

配点 : 300 点

問題文

ある地方に、1 から N の番号がついた N 個の街と、1 から M の番号がついた M 本の道路があります。

i 番目の道路は街 A_i と街 B_i を双方向に結び、長さは C_i です。

好きな街からスタートして同じ街を二度以上通らずに別の街へ移動するときの、通る道路の長さの和としてありえる最大値を求めてください。

制約

  • 2 \leq N \leq 10
  • 1 \leq M \leq \frac{N(N-1)}{2}
  • 1\leq A_i < B_i \leq N
  • (A_i,B_i) は相異なる
  • 1\leq C_i \leq 10^8
  • 入力は全て整数である

入力

入力は以下の形式で標準入力から与えられる。

N M
A_1 B_1 C_1
\vdots
A_M B_M C_M

出力

答えを出力せよ。

入力例 1

4 4
1 2 1
2 3 10
1 3 100
1 4 1000

出力例 1

1110

4\to 1\to 3\to 2 と移動すると、通る道路の長さの和は 1110 となります。

入力例 2

10 1
5 9 1

出力例 2

1

道路と繋がっていない街が存在するかもしれません。

入力例 3

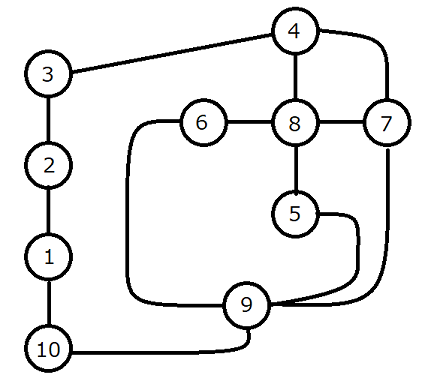
10 13
1 2 1
1 10 1
2 3 1
3 4 4
4 7 2
4 8 1
5 8 1
5 9 3
6 8 1
6 9 5
7 8 1
7 9 4
9 10 3

出力例 3

20

図

Score : 300 points

Problem Statement

A region has N towns numbered 1 to N, and M roads numbered 1 to M.

The i-th road connects town A_i and town B_i bidirectionally with length C_i.

Find the maximum possible total length of the roads you traverse when starting from a town of your choice and getting to another town without passing through the same town more than once.

Constraints

  • 2 \leq N \leq 10
  • 1 \leq M \leq \frac{N(N-1)}{2}
  • 1 \leq A_i < B_i \leq N
  • The pairs (A_i,B_i) are distinct.
  • 1\leq C_i \leq 10^8
  • All input values are integers.

Input

The input is given from Standard Input in the following format:

N M
A_1 B_1 C_1
\vdots
A_M B_M C_M

Output

Print the answer.

Sample Input 1

4 4
1 2 1
2 3 10
1 3 100
1 4 1000

Sample Output 1

1110

If you travel as 4\to 1\to 3\to 2, the total length of the roads you traverse is 1110.

Sample Input 2

10 1
5 9 1

Sample Output 2

1

There may be a town that is not connected to a road.

Sample Input 3

10 13
1 2 1
1 10 1
2 3 1
3 4 4
4 7 2
4 8 1
5 8 1
5 9 3
6 8 1
6 9 5
7 8 1
7 9 4
9 10 3

Sample Output 3

20

Figure