この問題を \(O(N(\log N)^2)\) 時間で解く方法について解説します。 標準的な D 問題相当より発展的な解説です。

この解説の内容はほとんど 熨斗袋さんの記事 に含まれます。

\((i,j)\to(i+1,j)\) および \((i,j)\to(i+1,j+1)\) の \(2\) 種類の移動のみができる平面があります。 \((0,0)\) から \((n,k)\) まで移動する経路を \(1\) つ与えられたとき、この経路より下側を通ることなく \((0,0)\) から \((n,k)\) へ向かう場合の数を \(O(n(\log n)^2)\) 時間で求めることができます。

より一般に、次の問題を \(O(n(\log n)^2)\) 時間で解くことができます。

\((0,0)\) から \((n,k)\) まで移動する経路 \(\bigl((i,Y _ i)\bigr) _ {1\leq i\leq n}\) と、長さ \(n+k\) の数列 \((\operatorname{dp} _ 0[j])_ {0\leq j\lt n+k}\) が与えられます。 \[\operatorname{dp} _ i[j]=\left\{\begin{matrix}\operatorname{dp} _ {i-1}[j]+\operatorname{dp} _ {i-1}[j-1]&\quad&(j\geq Y _ i)\\0&&(j\lt Y _ i)\end{matrix}\right.\] \(1\leq i\leq n\) においてこの漸化式を満たす \(\operatorname{dp} _ i[j]\) に対して、 \((\operatorname{dp} _ i[j]) _ {k\leq j\lt 2n+k}\) を求めなさい。ただし、\(j\lt0\) や \(n+k\leq j\) において \(\operatorname{dp} _ 0[j]=0\) とします。

たとえば、経路として \(\bigl((0,0),(1,0),(2,1),(3,1),(4,1)\bigr)\) を、\(\operatorname{dp} _ 0[j]\) として \((1,0,0,\ldots)\) を与えると、\(\operatorname{dp} _ i[j]\) の値は以下の図のようになります。

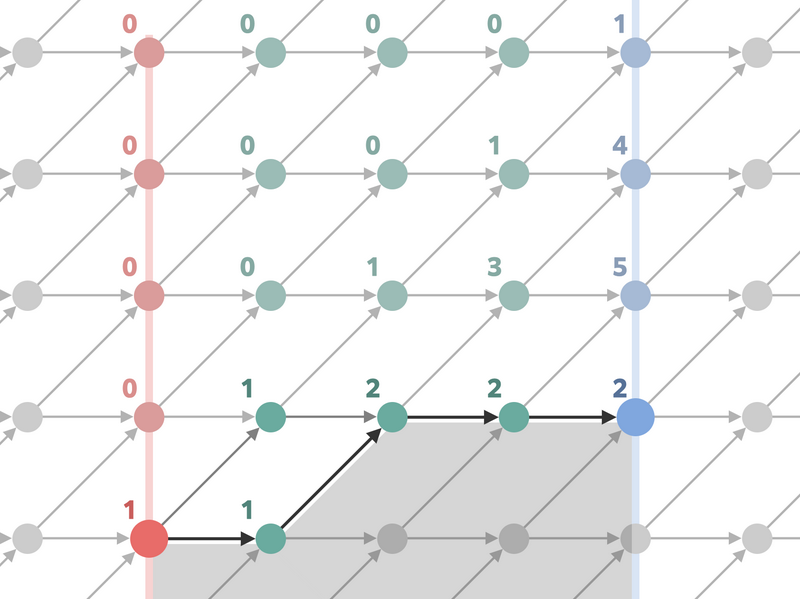
この問題は、下 \(k\) 行と上 \(n\) 行に分け、上 \(n\) 行はサイズ \(n\) の畳込みをし、下 \(k\) 行を再帰的に分割することで解くことができます。

計算量は、サイズ \(n\) の問題の計算量 \(T(n)\) に対して \[T(n)=n\log n+2T(n/2)\] となるため \(T(n)=O(n(\log n)^2)\) となります。

(, ), ? からなる文字列の ? をそれぞれ ( か ) のどちらかに置き換えることで成立した括弧列にする場合の数は、上の問題に帰着することができます。 よって、もとの問題を \(O(n(\log n)^2)\) 時間で解くことができました。

帰着やアルゴリズムの詳細は冒頭に挙げた記事を参照してください。

実装例は以下のようになります。 この実装例では \(\{0,1\}\) 列を管理するのに std::basic_string<bool> や std::basic_string_view<bool> などを用いています。

\(|S|=2\times10^5\) で全体のうち \(\dfrac78\) くらいが ? であるようなランダムケースにおいて \(150\operatorname{ms}\) 程度で実行が終了します。

#include <optional>
#include <vector>
#include <string>
#include <iostream>
#include <tuple>
#include <atcoder/convolution>

using namespace std;
using modint = atcoder::static_modint<998244353>;

// '(', ')', '?' からなる文字列を受け取り、
// https://noshi91.hatenablog.com/entry/2023/07/21/235339 の 2 つめのアルゴリズムにおける下端の形式に直す関数
// 返すのは 0, 1 からなる列で、下端の左から i 番目が右向きか右上向きかを表す
// ただし、どのように '?' を埋めても成立しない場合、nullopt を返す
optional<basic_string<bool>> wildcard_paren_string_to_floor(const string &S) {

    // v[i] = i 番目の ? までで '('の個数 - ')'の個数 はいくつ以上でなければいけないか
    vector<int> v = {0};
    {
        int x = 0;
        for (const auto c : S) {
            if (c == '(')
                --x;
            if (c == ')')
                ++x;
            if (c == '?')
                v.emplace_back(x);
            v.back() = max(v.back(), x);
        }

        // ワイルドカードがないのに括弧列として正しくなければ 0 通り
        if (v.size() == 1 && x != 0)
            return nullopt;
    }

    const int N = v.size(), M = v.back();

    // 通ることができない道を消す
    for (int i = 0; i < N; ++i)
        v[i] = v[i] + (1 & (v[i] ^ i)); // 偶奇
    for (int i = 0, j = 0; i < N; ++i) {
        j = max(j, v[i] + i);
        v[i] = j - i; // 降りられる限界
    }
    for (int i = N, j = M - N - 1; i--;) {
        j = max(j, v[i] - i);
        v[i] = j + i; // 登れる限界
    }

    // ワイルドカードが足りないので 0 通り
    if (v.front() != 0 || v.back() != M)
        return nullopt;

    // 下端の形式に直す
    basic_string<bool> result;
    result.reserve(N - 1);
    for (long i = 1; i < N; ++i)
        result.push_back(v[i] > v[i - 1]);

    return result;
}

// 再帰をするか DP テーブルを埋めるかの境界
constexpr unsigned threshold{64};

// https://noshi91.hatenablog.com/entry/2023/07/21/235339 の 2 つめのアルゴリズムを実行する関数
// FFT の結果の再利用はしない
pair<vector<modint>, vector<modint>> climbing_path_count(const vector<modint> &left, basic_string_view<bool> floor,
                                                         const vector<modint> &coefficients = {1}) {
    const unsigned N = floor.size(), M = reduce(floor.begin(), floor.end(), 0L), K = left.size();

    vector<modint> lower(left.begin(), left.begin() + min(M, K)); // 右端の下より下の部分
    vector<modint> upper(left.begin() + min(M, K), left.end()); // 右端の下から上の部分
    vector<modint> binomial = {1}; // 畳み込みに使う二項係数

    // 下部分の計算

    // N が小さいとき、DP テーブルを埋める O(N(N+K)) 時間
    if (N <= threshold) {
        unsigned l = 0, u = lower.size();
        for (const auto f : floor) {
            binomial.emplace_back();
            for (unsigned i = binomial.size(); --i;)
                binomial[i] += binomial[i - 1];

            lower.emplace_back();
            ++u;
            for (unsigned i = u; --i > l;)
                lower[i] += lower[i - 1];
            if (f)
                ++l;
        }
        for (unsigned i = l; i < u; ++i)
            swap(lower[i], lower[i - l]);
        lower.resize(u - l);
    }
    // N が大きいとき、再帰
    else {
        tie(lower, binomial) = climbing_path_count(lower, floor.substr(0, N / 2), binomial); // 左半分
        tie(lower, binomial) = climbing_path_count(lower, floor.substr(N / 2), binomial);    // 右半分
    }

    // 上部分の計算
    if (!upper.empty())
        upper = atcoder::convolution(upper, binomial);

    // 上下の結果を足し合わせる
    if (lower.size() < upper.size())
        swap(lower, upper);
    for (unsigned i = 0, i_upto = upper.size(); i < i_upto; ++i)
        lower[i] += upper[i];

    return make_pair(lower, convolution(coefficients, binomial));
}

int main() {
    string S;
    cin >> S;

    const auto floor = wildcard_paren_string_to_floor(S);

    if (!floor) {
        cout << 0 << endl;
        return 0;
    }

    // 左端の一番下のみに 1 を書き込んだときの右端の一番下が答え
    const auto&[a, b] = climbing_path_count({1}, floor.value());
    cout << a.front().val() << endl;

    return 0;
}