数 \(1\) の個数を \(C\) とします。

\(C=0\) のとき、最大流問題に帰着して解くことができます（詳細略）。

最大流問題に帰着するとき、ここではグラフが \(S \to {\rm odd} \to {\rm even}\to T\) となるように構成するものとします（正確な説明は省略、下図参照）。また、単に「最大流」と言った時、\(S\) から \(T\) への最大流を意味するものとします。頂点の名前と、対応する数を同一視します。

例

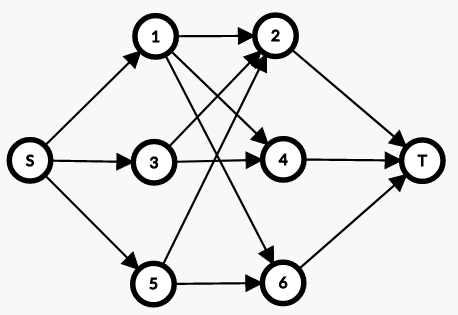
\(C>0\) の場合を考えます。

イメージとしては、\(1\) は使わないケースをベースに、\(1\) の使用を \(1\) 個解禁するごとに操作回数が何回増やせるかを考えます。（\(1\) 同士でペアを組むことで、明らかに \(2\) 個あたり \(1\) 回増えますが、それより良くなるかを考えます）

辺 \((S,1)\) の容量を \(C\) としたグラフを \(G_C\) とし、最大流量を \(F_C\) とします。
辺 \((S,1)\) の容量を \(0\) としたグラフを \(G_0\) とし、最大流量を \(F_0\) とします。

\(S\) から \(T\) への流量を固定したとき、辺 \((S,1)\) の流量はなるべく少なくなるようにするのが良いです（\(1\) は余ったら \(1\) 同士でペアを組めるので）。そこで、まず \(G_C\) の最大流の場合を考えてみます。つまり、「\(G_C\) の最大流のうち、辺 \((S,1)\) の流量の最小値」を \(f\) とし、\(f\) がいくらになるか考えます。

\(G_C\) の最大流のうち、 辺 \((S,1)\) の流量が最小になるものを任意に \(1\) つとります。ここから頂点 \(1\) を削除することで、流量 \(F_C-f\) の \(G_0\) のフローを作ることができます。従って \(F_C-f\leq F_0\) が成り立ちます。

\(G_0\) の最大流を任意に \(1\) つとります。これはそのまま \(G_C\) のフローだと思うことができます。このフローから始めて、Ford-Fulkerson のアルゴリズムにより、\(G_C\) の最大流を作るとき、辺 \((S,1)\) の流量は明らかに \(F_C-F_0\) 以下です。従って特に \(f \leq F_C-F_0\) となります。

以上より\(f=F_C-F_0\) となることがわかりました。このことから特に、辺 \((S,1)\) の容量 \(c\) を \(0\) から \(f\) の範囲で変化させたとき、最大流量は\(F_0+c\) となることがわかります。（そうでない \(c\) が存在すれば、それを \(G_0\) として上と同じ議論をすると矛盾）

このことはつまり、\(1\) 同士でペアを作る以外の操作回数の最大値は、\(1\) を使ってよい回数を \(c\) として、

• \(0\leq c \leq f\) のとき、\(F_0+c\)
• \( f\leq c\leq C\) のとき、\(F_C\)

となることを意味します。\(F_C\) までは \(1\) を \(1\) 個使うごとに操作回数が \(1\) 増やせるということなので、やれるだけやって損をせず、求める答えは
\(\displaystyle F_C+\left\lfloor\frac{1}{2}(C-(F_C-F_0))\right\rfloor\) になります。これは最大流問題を \(2\) 度解くことで求めることができます。

実装例(C++,ACL)