\(D_q\) 日目に \(i\) 番目の木から収穫を行う際、 もし \(i\) 番目の木から前回収穫を行ったのが \(B_i\) 日目であったとすると、 \(i\) 番目の木から今回収穫する木の実の個数は \(i \cdot (D_q- B_i)\) 個です。 このことから、本問題に対する次の素朴な解法が考えられます。

• まず、各 \(i = 1, 2, \ldots, N\) について木 \(i\) から最後に収穫を行った日を \(B[i]\) として記録するための、長さ \(N\) の配列 \(B\) を準備する。 便宜上、初期状態では \(B[1] = B[2] = \cdots = B[N] = 0\) とする。

• そして、\(q = 1, 2, \ldots, Q\) の順に下記を行う。

  • \(q\) 回目の収穫する木の実の合計数 \(\sum_{i = L_q}^{R_q} i \cdot (D_q - B[i])\) を出力する。
  • \(i = L_q, L_q+1, \ldots, R_q\) について、\(B[i] \leftarrow D_q\) と更新する。

この方法では、最悪時間計算量が \(\mathrm{\Theta}(NQ)\) となり、実行制限時間に間に合わせることは絶望的なため、 上記の方法の改良策として、\(B\) を下図のように各ブロック内の要素の値が等しいようないくつかのブロックに分割し、ブロックごとにまとめて収穫を行うことで高速化を図る方法を以下で述べます。

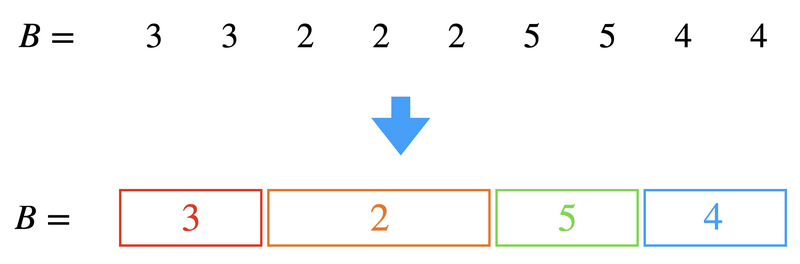
初期状態では、値が \(0\) のブロック \([1, N]\) のみがあります。 そして、各収穫の際には次の手順を行います。 （下図一段目から二段目のように、収穫区間 \([L_q, R_q]\) の両端にかかるブロックを適当に分割することにより、すべてのブロックは収穫区間に完全に含まれるか全く交わらないかのいずれかであると仮定します。）

• 収穫区間 \([L_q, R_q]\) に含まれるすべてのブロック \([l, r]\) （そのブロックの値を \(d\) とおく）にわたって、そのブロックから収穫する木の実の総数 \(\sum_{i = l}^{r} i \cdot (D_q - B[i]) = (D_q - d) (l+r) (r-l+1) / 2\) を計算し、その総和を出力する。
• 収穫区間 \([L_q, R_q]\) に含まれるすべてのブロックをすべて削除し、代わりに、値 \(D_q\) を持つ \(1\) つのブロック \([L_q, R_q]\) を追加する（下図二段目から三段目）。

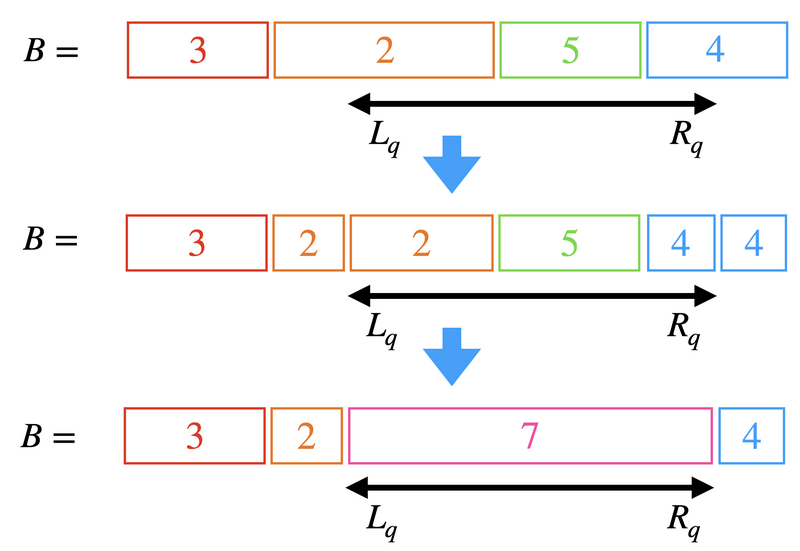
\(1\) 回の収穫で新たに追加されるブロックは \([L_q, R_q]\) の \(1\) 個であるため、アルゴリズム全体でブロックの挿入が行われる回数は \(\mathrm{O}(Q)\) 回です。 一度収穫の対象となったブロックは削除されるため、ブロックに対して収穫を行う回数はブロックが追加される回数以下であり、やはり \(\mathrm{O}(Q)\) 回です。 ブロックを平衡二分木で管理することによってブロックの追加や削除は \(\mathrm{O}(\log Q)\) 時間でできるため、上記の方法で本問題を\(\mathrm{O}(Q \log Q)\) 時間で解くことができます。