Let us consider the necessary and sufficient condition that a point \((a, b)\) is contained in the polygon \(P_j\). For example, suppose that \(P_j\) is a triangle illustrated as follows.

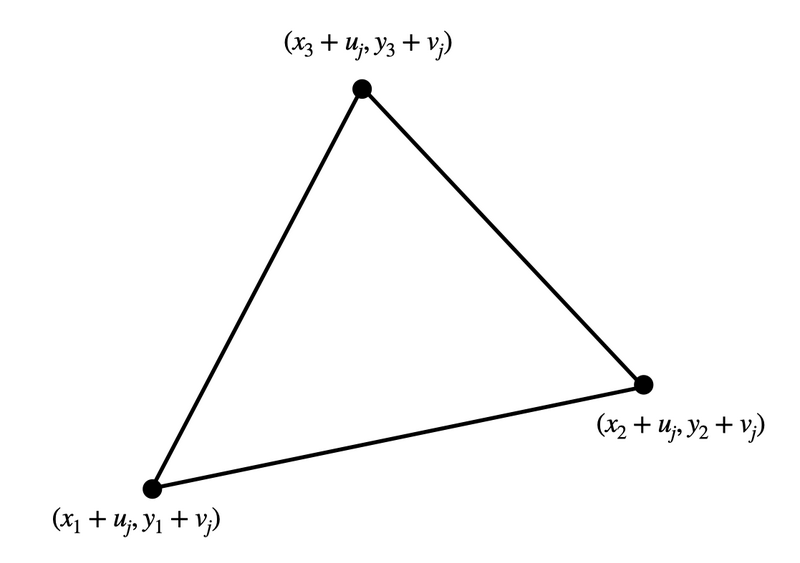
Here, a point \((a, b)\) is contained in \(P_j\) if and only if it is contained in all of the following three regions (including the boundaries).

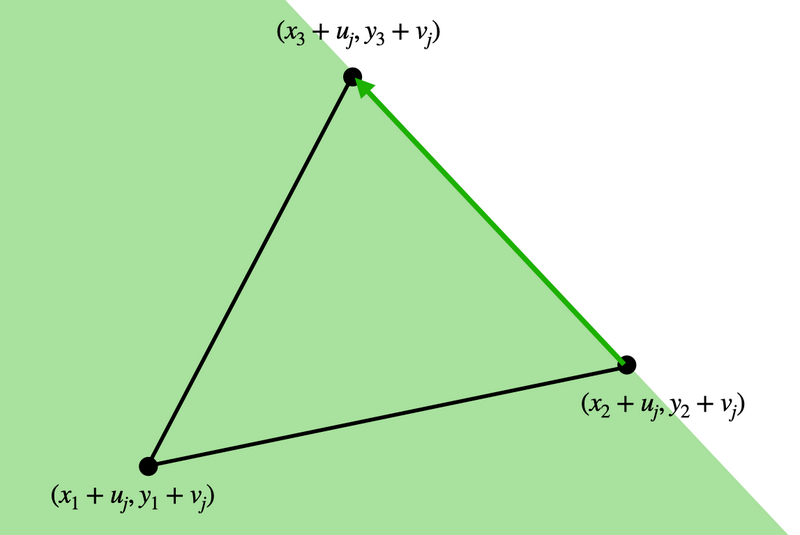
In general, a point \((a, b)\) is contained in the polygon \(P_j\) if and only if the following is satisfied for all \(i = 1, 2, \ldots, N\):

A point \((a, b)\) is contained in the left region of the directed segment from the point \((x_i+u_j, y_i + v_j)\) to the point \((x_{i+1}+u_j, y_{i+1} + v_j)\) (or the boundary).

“A point \((a, b)\) is contained in the left region of the directed segment from the point \((x_i+u_j, y_i + v_j)\) to the point \((x_{i+1}+u_j, y_{i+1} + v_j)\) (or the boundary)” if and only if the vector \(\left[\begin{matrix} a - (x_i+u_j)\\ b - (y_i+v_j)\\ \end{matrix}\right]\) of the directed segment from the point \((x_i+u_j, y_i+v_j)\) to the point \((x_{i+1}+u_j, y_{i+1}+v_j)\) and the vector \(\left[\begin{matrix} a - (x_i+u_j)\\ b - (y_i+v_j)\\ \end{matrix}\right]\) of the directed segment from the point \((x_i+u_j, y_i+v_j)\) to the point \((a, b)\) (see also the figure below) have the property that

\[ \left[\begin{matrix} x_{i+1} - x_i\\ y_{i+1} - y_i\\ \end{matrix}\right] \times \left[\begin{matrix} a - (x_i+u_j)\\ b - (y_i+v_j)\\ \end{matrix}\right] \geq 0. \tag{1} \]

Here, \(\left[\begin{matrix} p\\ q\\ \end{matrix}\right] \times \left[\begin{matrix} r\\ s\\ \end{matrix}\right] \) is defined to be the scalar value represented by \(ps - qr\).

We can transform the expression even further as

\[ \vec{Q_i} := \left[\begin{matrix} x_{i+1} - x_i\\ y_{i+1} - y_i\\ \end{matrix}\right], R_{i, j} := \left[\begin{matrix} x_{i+1} - x_i\\ y_{i+1} - y_i\\ \end{matrix}\right] \times \left[\begin{matrix} x_i+u_j\\ y_i+v_j\\ \end{matrix}\right] \]

so (1) is equivalent to

\[ \vec{Q_i} \times \left[\begin{matrix} a\\ b\\ \end{matrix}\right] \geq R_{i, j}. \tag{2} \]

Thus, in order to determine if a point \((a, b)\) is contained in \(P_j\), it is sufficient to determine if (2) holds for all \(i = 1, 2, \ldots, N\). Therefore, in order to determine if a point \((a, b)\) is contained in all of \(P_1, P_2, \ldots, P_M\), it is sufficient to determine if (2) holds for all pairs of \(i = 1, 2, \ldots, N\) and \(j = 1, 2, \ldots, M\).

However, this method requires checking if (2) is satisfied for all \(NM\) pairs of \((i, j)\) for each point \((a, b)\), but it is hopeless it can be processed in time for each point \((a, b)\), but it is hopeless it can be processed in time.

Here, note that the left hand side of (2) is independent of \(j\) and only dependent on \(i\). Thus, instead of checking if (2) holds for all pairs of \(i = 1, 2, \ldots, N\) and \(j = 1, 2, \ldots, M\), it is sufficient to check if it holds for all \(i = 1, 2, \ldots, N\) that

\[ \vec{Q_i} \times \left[\begin{matrix} a\\ b\\ \end{matrix}\right] \geq \max_{j = 1, 2, \ldots, M} R_{i, j}. \tag{3} \]

So, we first spend \(\mathrm{O}(NM)\) time to precalculate \(\max_{j = 1, 2, \ldots, M} R_{i, j}\) for all \(i = 1, 2, \ldots, N\). Then we can determine if (3) is satisfied for a given point \((a, b)\) for all \(i = 1, 2, \ldots, N\) in an \(\mathrm{O}(N)\) time for each point.

Therefore, the problem has been solved in a total of \(\mathrm{O}(N(M + Q))\) time.

The following is a sample code in C++.

#include <iostream>
using namespace std;
typedef long long ll;
const ll inf = 1e18;

ll n, m, q;
ll x[55], y[55];
ll u[200005], v[200005];
ll Q1[55], Q2[55], R[55];

ll cross(ll p, ll q, ll r, ll s){
  return p*s - q*r;
}

int main(void)
{
  cin >> n;
  for(int i = 1; i <= n; i++) cin >> x[i] >> y[i];
  x[n+1] = x[1], y[n+1] = y[1];
  cin >> m;
  for(int i = 1; i <= m; i++) cin >> u[i] >> v[i];
  
  for(int i = 1; i <= n; i++){
    Q1[i] = x[i+1]-x[i], Q2[i] = y[i+1]-y[i], R[i] = -inf;
    for(int j = 1; j <= m; j++){
      R[i] = max(R[i], cross(x[i+1]-x[i], y[i+1]-y[i], x[i]+u[j], y[i]+v[j]));
    }
  }
  
  cin >> q;
  ll a, b;
  for(int k = 1; k <= q; k++){
    cin >> a >> b;
    bool ans = true;
    for(int i = 1; i <= n; i++) if(cross(Q1[i], Q2[i], a, b) < R[i]) ans = false;
    if(ans) cout << "Yes" << "\n";
    else cout << "No" << "\n";
  }
  
  return 0;
}