点 \((a, b)\) が多角形 \(P_j\) に含まれる必要十分条件を考えます。 例として、\(P_j\) が次の図のような三角形の場合を考えます。

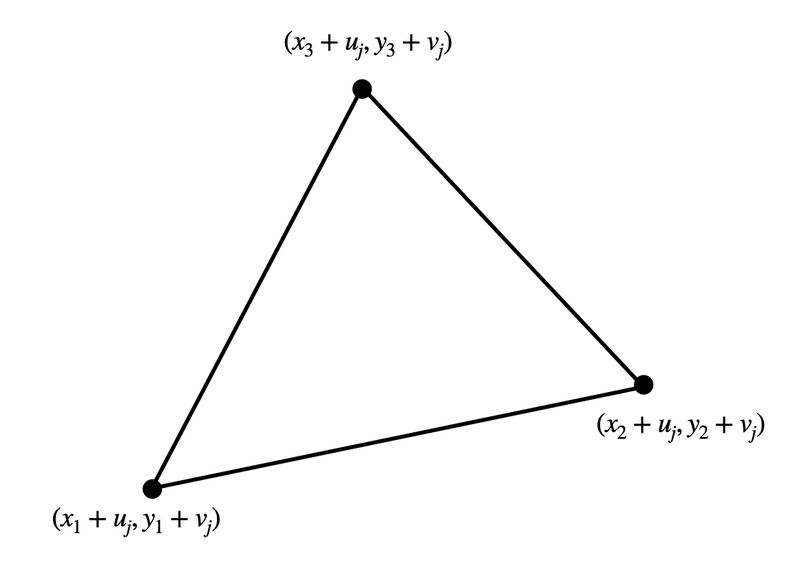
このとき、点 \((a, b)\) が \(P_j\) に含まれることは、次の \(3\) つの図で塗りつぶされた \(3\) つの領域（境界上も含む）のすべてに点 \((a, b)\) が含まれることと同値です。

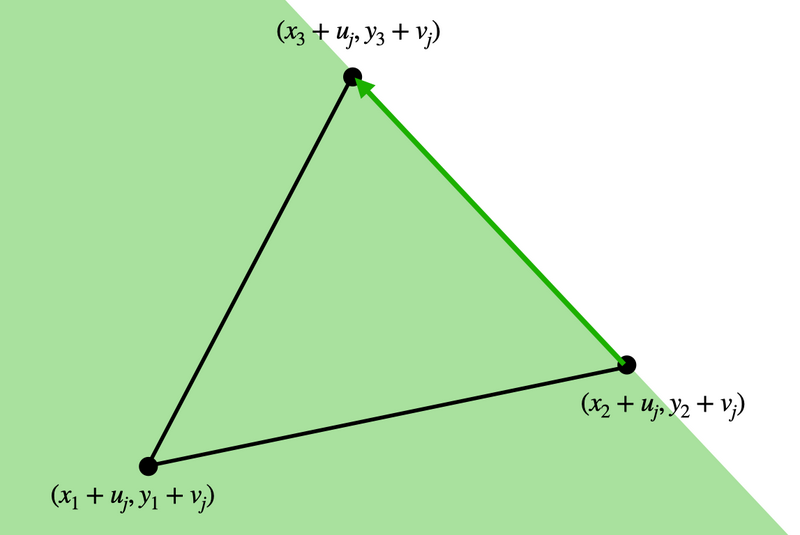
一般に、点 \((a, b)\) が多角形 \(P_j\) に含まれることは、すべての \(i = 1, 2, \ldots, N\) について、

点 \((a, b)\) は点 \((x_i+u_j, y_i + v_j)\) から点 \((x_{i+1}+u_j, y_{i+1} + v_j)\) へ向かう有向線分の左側にある領域（または境界）に含まれる

ことと同値です。

「点 \((a, b)\) が点 \((x_i+u_j, y_i+v_j)\) から点 \((x_{i+1}+u_j, y_{i+1}+v_j)\) へ向かう有向線分の左側にある領域（または境界）に含まれる」ことは、 点 \((x_i+u_j, y_i+v_j)\) から点 \((x_{i+1}+u_j, y_{i+1}+v_j)\) への有向線分で表されるベクトル \(\left[\begin{matrix} a - (x_i+u_j)\\ b - (y_i+v_j)\\ \end{matrix}\right]\) と、 点 \((x_i+u_j, y_i+v_j)\) から点 \((a, b)\) への有向線分で表されるベクトル\(\left[\begin{matrix} a - (x_i+u_j)\\ b - (y_i+v_j)\\ \end{matrix}\right]\) （下図参照）によって、

\[ \left[\begin{matrix} x_{i+1} - x_i\\ y_{i+1} - y_i\\ \end{matrix}\right] \times \left[\begin{matrix} a - (x_i+u_j)\\ b - (y_i+v_j)\\ \end{matrix}\right] \geq 0 \tag{1} \]

と言い換えられます。 ただし、\(\left[\begin{matrix} p\\ q\\ \end{matrix}\right] \times \left[\begin{matrix} r\\ s\\ \end{matrix}\right] \) は \(ps - qr\) で定義されるスカラー量とします。

さらに整理すると、

\[ \vec{Q_i} := \left[\begin{matrix} x_{i+1} - x_i\\ y_{i+1} - y_i\\ \end{matrix}\right], R_{i, j} := \left[\begin{matrix} x_{i+1} - x_i\\ y_{i+1} - y_i\\ \end{matrix}\right] \times \left[\begin{matrix} x_i+u_j\\ y_i+v_j\\ \end{matrix}\right] \]

によって、(1) は

\[ \vec{Q_i} \times \left[\begin{matrix} a\\ b\\ \end{matrix}\right] \geq R_{i, j} \tag{2} \]

と表せます。

よって、点 \((a, b)\) が \(P_j\) に含まれるかを判定するには、 すべての \(i = 1, 2, \ldots, N\) で (2) が成り立つかを判定すれば良いです。 したがって、点 \((a, b)\) が \(P_1, P_2, \ldots, P_M\) のすべてに含まれるかを判定するには、すべての \(i = 1, 2, \ldots, N\) と \(j = 1, 2, \ldots, M\) の組について (2) が成り立つかを判定すれば良いです。

しかし、この方法では各点 \((a, b)\) について \(NM\) 個の \((i, j)\) の組に対して (2) が成り立つかを判定する必要があるため、実行制限時間に間に合わせることは絶望的です。

ここで、(2) の左辺は \(j\)によらず \(i\) のみから定まることに注目すると、すべての \(i = 1, 2, \ldots, N\) と \(j = 1, 2, \ldots, M\) の組について (2) が成り立つかを判定するのではなく、 すべての \(i = 1, 2, \ldots, N\) で

\[ \vec{Q_i} \times \left[\begin{matrix} a\\ b\\ \end{matrix}\right] \geq \max_{j = 1, 2, \ldots, M} R_{i, j} \tag{3} \]

が成り立つかを確かめれば十分です。

そこで、まず \(\mathrm{O}(NM)\) 時間の前計算によってすべての \(i = 1, 2, \ldots, N\) について \(\max_{j = 1, 2, \ldots, M} R_{i, j}\) をあらかじめ求めておきます。 それによって、与えられた点 \((a, b)\) についてすべての \(i = 1, 2, \ldots, N\) で (3) が成り立つかの判定は各点あたり \(\mathrm{O}(N)\) 時間で行えます。

以上より、本問題を \(\mathrm{O}(N(M + Q))\) 時間で解くことができます。

以下に、C++ 言語による正解例を記載します。

#include <iostream>
using namespace std;
typedef long long ll;
const ll inf = 1e18;

ll n, m, q;
ll x[55], y[55];
ll u[200005], v[200005];
ll Q1[55], Q2[55], R[55];

ll cross(ll p, ll q, ll r, ll s){
  return p*s - q*r;
}

int main(void)
{
  cin >> n;
  for(int i = 1; i <= n; i++) cin >> x[i] >> y[i];
  x[n+1] = x[1], y[n+1] = y[1];
  cin >> m;
  for(int i = 1; i <= m; i++) cin >> u[i] >> v[i];
  
  for(int i = 1; i <= n; i++){
    Q1[i] = x[i+1]-x[i], Q2[i] = y[i+1]-y[i], R[i] = -inf;
    for(int j = 1; j <= m; j++){
      R[i] = max(R[i], cross(x[i+1]-x[i], y[i+1]-y[i], x[i]+u[j], y[i]+v[j]));
    }
  }
  
  cin >> q;
  ll a, b;
  for(int k = 1; k <= q; k++){
    cin >> a >> b;
    bool ans = true;
    for(int i = 1; i <= n; i++) if(cross(Q1[i], Q2[i], a, b) < R[i]) ans = false;
    if(ans) cout << "Yes" << "\n";
    else cout << "No" << "\n";
  }
  
  return 0;
}