\(dp[\) \(i\) 日目までの取引を終えた状態 \(][\) 現状 \(j\) 株持っている \(]=\{\) 所持金の増加額の最大値 \(\}\) というDPを行えばこの問題を \(O(N^2)\) で解くことができます。取引終了時に株を残しておくメリットがないことから、答えは \(dp[N][0]\) となります。

サンプル1 を使い、このDPを観察してみましょう。

サンプル1 の入力:

8
2 5 4 3 7 1 8 6

上から \(i\) 行目、左から \((j-1)\) 列目に \(dp[i][j]\) を出力した数表:

 0  -2
 3  -2  -7
 3  -1  -6 -11
 3   0  -4  -9 -14
 7   3  -2  -7 -14 -21
 7   6   2  -3  -8 -15 -22
14  10   5   0  -7 -14 -22 -30
16  11   6   0  -6 -13 -20 -28 -36

横方向に等差数列がいくつか見えるので、隣接項の公差をとってみましょう。
上から \(i\) 行目、左から \(j\) 列目に \(dp[i][j-1]-dp[i][j]\) を出力した数表:

2
5 5
4 5 5
3 4 5 5
4 5 5 7 7
1 4 5 5 7 7
4 5 5 7 7 8 8
5 5 6 6 7 7 8 8

\(dp[N][0]\) を求めるためにこの数表たちを観察すると、以下の解法が成立しそうに見えます。

• まず、 多重集合 \(M=\{A_1\}\) を用意し、答え \(R\) を \(0\) で初期化する。
• \(i=2,3,\dots,N\) に対して、順に以下を行う。
  • もし、 \(M\) の最小値 \(m\) より \(A_i\) の方が大きければ、 \(R\) に \(A_i-m\) を加算し、 \(M\) から \(m\) を (\(1\) つ) 削除する。その後、 \(M\) に \(A_i\) を \(2\) つ追加する。
  • そうでない場合、 \(M\) に \(A_i\) を \(1\) つ追加する。

実際、この解法は正しいです。ここからは、解法の正当性を説明します。

横軸に \(j\) 、縦軸に \(dp[i][j]\) の値をとりプロットした折れ線が上に凸になることを仮定します(\(dp[1]\) の時点では、これは明らかに正しいです。)
\(dp[i]\) から \(dp[i+1]\) へと、どのような遷移が行われるか考察します。
\(dp[i+1][j]\) は、以下の \(3\) つの \(\max\) をとったものとなります。

• \(dp[i][j]\) ( \(i+1\) 日目に何もしなかったケース)
• \(dp[i][j-1]-A_{i+1}\) ( \(i+1\) に株を買ったケース)
• \(dp[i][j+1]+A_{i+1}\) ( \(i+1\) に株を売ったケース)

これを折れ線の平行移動に対応させると、それぞれ

• \(dp[i]\) (この折れ線を \(dp\) とする)
• \(dp[i]\) を右に \(1\) 、下に \(A_{i+1}\) 移動させた折れ線 (この折れ線を \(dp_-\) とする)
• \(dp[i]\) を左に \(1\) 、上に \(A_{i+1}\) 移動させた折れ線 (この折れ線を \(dp_+\) とする)

に対応します。

以下の図は、 \(A=(4,2,2,1,1,1,3)\) であったとき、 \(dp[6]\) から \(dp[7]\) を求める際の各折れ線です。

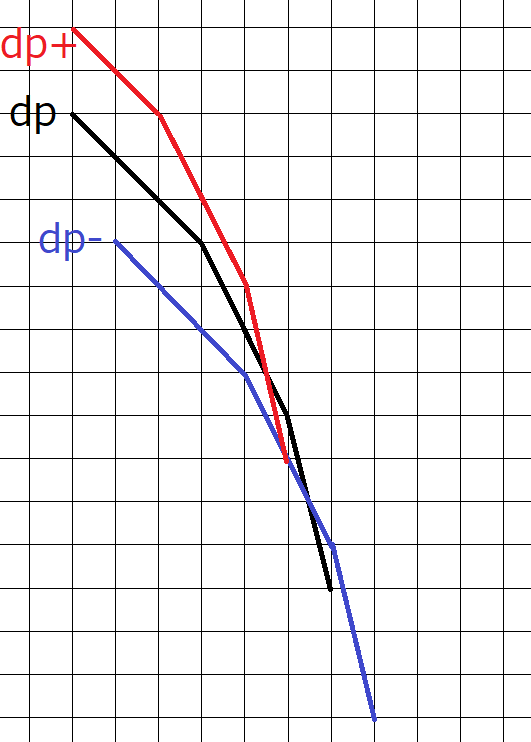
まず、 \(dp\) と \(dp_-\) とを比較し、それらの \(\max\) を取った折れ線 \(L_-\) を考えてみましょう。

• 両折れ線の傾きが \(-A_{i+1}\) 以上の部分については、 \(dp\) が \(dp_-\) 以上の位置にあるので、 \(L_-\) と \(dp\) が一致します。
• 両折れ線の傾きが \(-A_{i+1}\) 未満の部分については、 \(dp_-\) が \(dp\) より上の位置にあるので、 \(L_-\) と \(dp_-\) が一致します。
• この \(2\) つの部分の間に、折れ線 \(L_-\) 上に、傾きが \(-A_{i+1}\) の (横幅 \(1\) の) 線分が入ります。ここで、 \(dp_-\) が \(dp\) より上側に来ます。

次に、 \(dp\) と \(dp_+\) とを比較して同様の考察を行った折れ線 \(L_+\) について検討します。

• 両折れ線の傾きが \(-A_{i+1}\) 以上の部分については、 \(dp_+\) が \(dp\) 以上の位置にあるので、 \(L_+\) と \(dp_+\) が一致します。
• 両折れ線の傾きが \(-A_{i+1}\) 未満の部分については、 \(dp\) が \(dp_+\) より上の位置にあるので、 \(L_+\) と \(dp\) が一致します。
• この \(2\) つの部分の間に、折れ線 \(L_+\) 上に、傾きが \(-A_{i+1}\) の (横幅 \(1\) の) 線分が入ります。ここで、 \(dp\) が \(dp_+\) より上側に来ます。

最終的な遷移後の \(dp\) は \(L_-\) と \(L_+\) の \(\max\) を取ったものであるため、出来上がる \(dp\) は遷移前の \(dp\) に傾き \(-A_{i+1}\) の横幅が \(1\) または \(2\) の線分を挿入して適切に平行移動したような形になります。

この議論を整理すると、先程示した解法の正当性を示すことができます。

実装例(C++):

#include<bits/stdc++.h>

using namespace std;

int main(){
  int n;
  cin >> n;
  vector<long long> a(n);
  for(auto &nx : a){cin >> nx;}
  long long res=0;
  priority_queue<long long,vector<long long>,greater<long long>> pq;
  pq.push(a[0]);
  for(int i=1;i<n;i++){
    if(pq.top()<a[i]){
      res+=(a[i]-pq.top());
      pq.pop();
      pq.push(a[i]);
    }
    pq.push(a[i]);
  }
  cout << res << '\n';
  return 0;
}