記号の定義

正整数 \(N\) と素数 \(p\) に対して \({\rm ord}_p(N)\) を、\(N\) が \(p\) で割り切れる回数とします。

元の問題は素数べきごとに分解することで、次のようになります。

問題(☆)：素数 \(p\)、正整数 \(e,K\)、\(0\) 以上 \(p^e\) 未満の整数 \(N\)、正整数 \(\rm MOD\) が与えられる。\(0\) 以上 \(p^e\) 未満の整数からなる長さ \(K\) の数列 \(A\) であって、\(\prod A_i =N \bmod p^e\) となるもの個数を \(\bmod {\rm MOD}\) で求めよ。

この問題は、実は次の問題が解ければ解くことができます。

問題(★)：素数 \(p\)、正整数 \(e,K\)、正整数 \(\rm MOD\) が与えられる。\(0\) 以上 \(p^e\) 未満の整数からなる長さ \(K\) の数列 \(A\) であって、\(\prod A_i=p^x \bmod p^e\) となるもの個数を各 \(x=0,\ldots,e-1\) に対して \(\bmod {\rm MOD}\) で求めよ。

問題(★)及び問題(☆)が \(O(e+\log K)\) で解ける(注)ことを以下で示します。以下では、断りなく \(A\) という記号を使った場合、「\(0\) 以上 \(p^e\) 未満の整数からなる長さ \(K\) の数列」を指すものとします。

注釈

• \((e-1)!\) と \(\rm MOD\) が互いに素であることを仮定します。
• \(\bmod {\rm MOD}\) での四則計算を \(O(1)\) とします。また、\(p,K\) が巨大な場合、最初に1度だけ、これらの \(\bmod {\rm MOD}\) を求める時間が別途かかります。
• 問題(☆)を解くには、問題(★)を解く計算量に加え、別途 \({\rm ord}_p(N)\) を求める時間がかかります。これは \(N,p\) が関わる乗除算が \(O(e)\) 回必要です。

問題(★)が解ければ問題(☆)も解けること

まず、次の主張を示します。

主張(◆)：整数 \(X,Y\) が \({\rm ord}_p(X)={\rm ord}_p(Y)< e\) を満たすならば、 \(\prod A_i =X\bmod p^e\) となる数列の個数と \(\prod A_i =Y\bmod p^e\) となる数列の個数は等しい。

証明

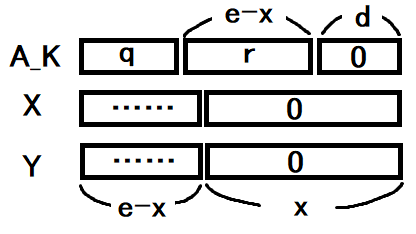
\(0\leq x< e\) となる \(x\) と、\({\rm ord}_p(X)={\rm ord}_p(Y)=e\) を満たす正整数 \(X,Y\) を任意に取る。\(\prod A_i =X\bmod p^e\) となる数列を任意に取る。\(p\) と互いに素かつ \(p^{e-x}\) 未満の正整数 \(r\) と整数 \(q\) によって、\(A_K=p^d(qp^{e-x}+r)\) と一意に表すことができる。ここで、\(r'\) を、\(\frac{Y}{p^x}r=\frac{X}{p^x}r' \bmod p^{e-x}\) を満たす \(p^{e-x}\) 未満の唯一の正整数とし、\(A_K\) を\(p^d(qp^{e-x}+r')\) に置き換えると、新たにできた数列は \(\prod A_i =Y\bmod p^e\) を満たす。\(r'\) の構成から、この変換は全単射である。(証明終)

直感的な説明

\(p\) 進法で表したとき、\(X,Y\) は trailing zero を除くと \(e-x\) 桁なので、\(A_K\) の(trailing zero を除いた) 下 \(e-x\) 桁を調整すれば、\({\rm ord}_p\) が変わらない範囲でなんでも作れます。

問題(★)が解けたとき、問題(☆)は次のように解けます。

• \(N\neq 0\) のとき、\(x={\rm ord}_p(N)\) に関する問題(★)の答えが求める値そのものです。
• \(N=0\) のとき、全てのケース \((p^e)^K\) 通りから、\({\rm ord}_p(\prod A_i)< e\) のケースを引いたものが答えです。明らかに \(O(e+\log K)\) で求めることができます。

問題(★)を解く

求める答えは \(\binom{K+x-1}{x}(p-1)^{K-1} p^{(e-1)(K-1)}\) になります。

証明

\(0\) 以上 \(p^e\) 未満の整数 \(n\) であって、\({\rm ord}_p(n)=x\) を満たすものは \((p-1)p^{e-1-x}\) 個存在する。したがって、主張(◆)より、\({\rm ord}_p(\prod A_i)=x\) を満たす数列が \(\binom{K+x-1}{x}(p-1)^K p^{(e-1)K-x}\) 個存在することを示せばよい。\(c_i={\rm ord}_p(A_i)\) とした数列 \(c\) を考える。\({\rm ord}_p(\prod A_i)=x\) であることと、\(\sum c_i=x\) であることは同値であるため、まず \(\sum c_i=x\) を満たす非負整数列 \(c\) を任意にとり、その後 \(c_i={\rm ord}_p(A_i)\) を満たす \(A_i\) を取ることにする。\(c\) を決めたとき、各 \(i\) について \(A_i\) の取りうる値は(\(c_i< e\) なので) \((p-1)p^{e-1-c_i}\) 通りあり、\(c_i={\rm ord}_p(A_i)\) を満たす数列 \(A\) は \(\prod (p-1)p^{e-1-c_i}=(p-1)^K p^{(e-1)K-x}\) 個ある。これは \(c\) に依らない。\(c\) は \(\binom{K+x-1}{x}\) 通りあるため、求めるものは \(\binom{K+x-1}{x}(p-1)^K p^{(e-1)K-x}\) 個ある。

図解

\(x\) の昇順に、逆元を \(O(1)\) で求めながら二項係数を計算することで、全体で \(O(\log K+e)\) で求めることができます。

また、\(\rm MOD\) が素数であれば、\(K\bmod ({\rm MOD}-1)\) を予め計算しておくことで、\(O(\log K)\) を \(O(\log\min\{K,{\rm MOD}\})\) にできます。

以上から、例えば次のような制約でも元の問題を解くことができます：

制約

• \(M=p^m,N=p^n\) であり、\(N,M\) の代わりに \(p,n,m\) が与えられる。
• \(1 \leq K \leq 10^{1000000}\)
• \(2 \leq p \leq 10^{1000000}\)
• \(p\) は素数
• \(0 \leq n < m \leq 10^{6}\)