If there are two rectangles

We first consider the following problem: “Can we place two good rectangles whose areas are at least \(S\) and \(T\), respectively, so that they do not overlap with each other?”

We will prove that the following conjecture is true.

• For a placement that satisfies the conditions, there exists a line \(l\) parallel to the \(x\) axis or the \(y\) axis such that:
  • \(l\) does not pass through the interior of any rectangle.
  • By dividing \(xy\)-plane into two parts by \(l\), each region has one rectangle.

In the diagram above, one of the rectangles are shown as the gray part. Then, the other rectangle does not overlap with two or more red regions (or otherwise, it also overlaps with the gray rectangle.) Therefore, the line obtained by elongating one of the four edges of the gray rectangle satisfies the conditions described above.

If there exists \(l\) that is parallel to \(x\), then we can assume that \(l\) is represented by the equation \(y = \left \lceil \frac{S}{X} \right \rceil\). Also, if there exists \(l\) that is parallel to \(y\), then we can assume that \(l\) is represented by the equation \(x = \left \lceil \frac{S}{Y} \right \rceil\). By checking these two cases, we can find the answer.

If there are three rectangles

As with the case with two rectangles, we will prove the following conjecture.

• For a placement that satisfies the conditions, there exists a line \(l\) parallel to the \(x\) axis or the \(y\) axis such that:
  • \(l\) does not pass through the interior of any rectangle.
  • By dividing \(xy\)-plane into two parts by \(l\), one of them has one rectangle and the other has two rectangles.

First, take two rectangles arbitrarily, and take the line \(l\) that satisfies the conditions described in “if there are two rectangles.” Without loss of generality, we can assume that \(l\) is parallel to the \(y\) axis.

If at most one of the dotted lines in the diagram above passes through the other rectangle, then one of the dotted lines satisfies the conditions. If both of them passes through the interior of the other rectangle, then the blue regions on the left and right of the other rectangle (shown in red in the diagram below) overlaps with neither of the gray rectangles. Therefore, one of the lines obtained by elongating the edges of the red rectangle that is parallel to the \(x\) axis satisfies the conditions.

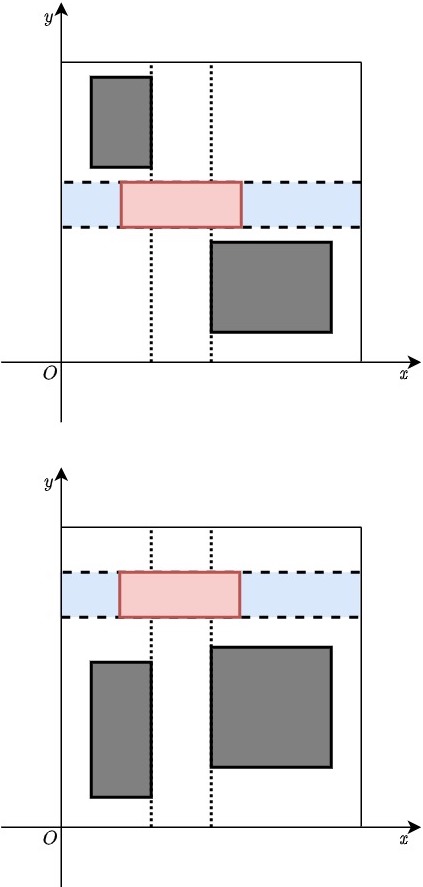
Hence, it is sufficient to search the following patterns exhaustively:

• whether \(l\) is parallel to \(x\) axis or \(y\) axis;
• when the \(xy\) plane is divided into two parts, which rectangle is included in the region that has only one rectangle.

For the region that contains two rectangle, we can find the answer by solving the problem for the case when “there are two rectangles.”

Sample code