This editorials is rather like a User’s Editorials that illustrates the “intuition” of one of the solution, Alien DP.
Please refer to the editorial by kyopro_friends for the explanation of the problem itself. For mathematical explanation of Alien DP, please refer to the article of Kyopro Encyclopedia of Algorithms by noshi91 (in Japanese).

Now, this problem can be rephrased as follows.

Given \(N\) balls, you will paint \(R\) balls in black so that no two consecutive balls are painted in black. If you paint Ball \(i\) in black, you will obtain a score of \(A_{i-1} + A_{i}\). What is the maximum score?

\(N \leq 2 \times 10^5, R \leq \left\lfloor \frac{N}{2} \right\rfloor\)

Here we will take an example for \(N = 11, A = (3,1,4,1,5,9,2,6,5,3)\). In that case, denoting by \(f(x)\) the answer for \(R = x\), we can obtain through an experiment the values of \(f(x)\) for for \(x = 0,1,\dots,5\) and the graph of \(f(x)\) with adjacent plots connected with segments as follows.

x	0	1	2	3	4	5
f(x)	0	14	25	30	35	39

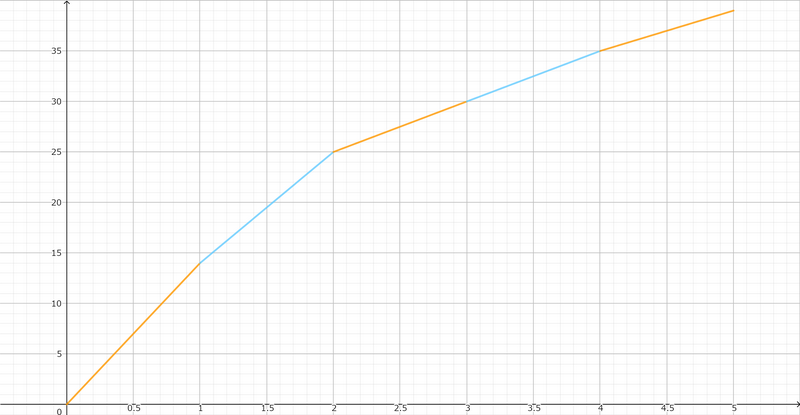
As you can see in the graph, \(f(x)\) is a concave function. This can be proved for general \(N\) and \(A\). (Someone else told me this.)

• Brief proof: It is sufficient to prove \(f(k-1) + f(k+1) \leq 2 f(k)\). Let \((a_1,\ldots,a_{x-1})\) and \((b_1,\ldots,b_{x+1})\) be the indices achieving the optimal solution for \(x-1\) and \(x+1\), respectively, and let \(c=(c_1,\ldots, c_{2x})\) be a concatenation of \(a\) and \(b\), sorted. Then \((c_1,c_3,\dots,c_{2k-1})\) and \((c_2,c_4,\dots,c_{2k})\) are both valid combinations of \(k\) choices, and at least one of them has the score of at least \(\frac{f(k-1) + f(k+1)}{2}\).

We want to find the value of \(f(R)\), but if we do DP (Dynamic Programming) over the number of balls and position, it will take \(\mathrm{\Omega}(N^2)\) time. This is because the DP table itself has the size of \(\mathrm{O}(N^2)\), so the lower bound of computation time is in the order of \(N^2\) as long as we perform naive DP.

It’s sudden but let’s think totally differently. First let’s solve the following problem.

Given \(N\) balls, you will paint some balls in black so that no two consecutive balls are painted in black. If you paint Ball \(i\) in black, you will obtain a score of \(A_{i-1} + A_{i}\). Also, every time you paint a ball, the score decreases by 8. What is the maximum score? Also, at most how many balls are painted when the score is maximum?

This problem can be solved with a DP in a total of \(\mathrm{O}(N)\) time. Plus, the answer for this problem is obviously

\[\max_{x=0,1,\dots,5} f(x) - 8x.\]

For the previous example, the score reaches the maximum value of \(9\) when \(x = 2\). Let us interpret this equation as a graph. The knowledge of high-school math tells us that the value \(x\) satisfying the equation above can be represented as the uppermost intersection of the graphs \(y = f(x)\) and \(y = 8x + m\). Visually it can be shown as follows.

As you can see, when the cost for painting one ball \(C\) is fixed, the desired answer corresponds to the \(x\) coordinate of the intersection point of two graphs \(y = f(x)\) and \(y = Cx + m\). With this property, we can find \(f(R)\) without naively filling the DP table, which is the essential part of Alien DP we are going to explain now.

Now let’s go back to the original problem. First, let \(T = f(R) - f(R - 1)\). If we do DP with \(C\) fixed, by dropping a line of slope \(C\) onto the graph, \(T\), \(C\) and \(R\) satisfies the following relationships:

• If \(C \leq T\): the maximum number of choice is greater than or equal to \(R\)
• If \(C \gt T\): the maximum number of choice is less than \(R\)

Therefore, we can do binary search over \(C\) to find the value of \(T\). In other words, we have found the value \(C\) such that the optimal number of choice is \(K\), so once we found \(T\), we can assume \(C = T\) and the answer for the original problem is the score obtained by DP, with \(TR\) added.

As explained so far, the “intuition” of Alien DP is to substitute the constraints of “choosing exactly \(R\) elements” to “choosing one element costs \(C\) each,” find appropriate \(C\) by doing binary search over \(C\), and finally finding \(f(R)\).

Here is a sample code.

We will finish this editorials with some notes.

• When implementing, we have to be careful of the values around boundary, or it may cause a bug if there is no \(C\) that the number of choices is \(R\).
  For example, in the example above, both \(f(3)-f(2)\) and \(f(4) - f(3)\) are \(5\), so there doesn’t exist such \(C\) that the optimal number is \(3\). In such case, if we assume precedence only based on DP, we may not be able to obtain correct \(T\). This can be resolved by, for example, when doing DP, “tie-breaking the combinations of the same score by the number of painted balls.”
• If we use decimals for binary search, we cannot obtain correct answer for large \(N\) and \(A\). Although many materials of Alien DP does binary search over decimals, this problem has the maximum answer of as large as \(2 \times 10^{14}\), which requires very high precision, accompanied by the necessity of subtraction of values with different signs, making it unable to compute \(C\) correctly.
  In this problem, the issue can be resolved by doing binary search for \(C\) over integers, using the property that the slope is integral. In case of decimals, we do not have to be nervous about the boundaries, but in case of integers, we may have to be cautious in implementing, so be careful.