必要なら赤と青を入れ替えることで、\(R\leq N/2\) としてよいです。

最適解において赤いランプが隣り合うことはありません。

赤いランプが隣り合っている箇所が存在する場合、適当な操作によって報酬を増やせることを示します。
ランプ \(i\) とランプ \(i+1\) がともに赤であるような最大の \(i\) をとります。\(j\geq i\) であって、ランプ \(j\) とランプ \(j+1\) がともに青であるような最小の \(j\) を取ります（存在しないときは \(j=N\) とする）。このとき、ランプ \(i+1\) からランプ \(j\) までのランプの色を反転させることで、ほとんどの場合で赤いランプの個数を変えることなく報酬を増加させることができます。
唯一の例外は \(j=N\) かつランプ \(N\) が赤い場合であり、このときは反転操作により赤いランプの個数が \(1\) 個減ってしまいます。しかし、このときはランプ \(1\) から \(i-1\) までのいずれかに青いランプが \(3\) 連続している箇所が存在するか、ランプ \(1,2\) がともに青であることが示せるため、そのようなものの \(1\) つを青から赤に変えることで、やはり赤いランプの個数を変えることなく報酬を増加させることができます。

したがって問題は次のように読み替えられます。

「\(1\) から \(N\) の番号がついた \(N\) 個ランプのうちちょうど \(R\) 個を赤く、残りを青くする。ランプ \(i\) を赤くすると \(B_i\) の報酬を得る。赤いランプを連続させることができないとき、報酬の合計の最大値を求めよ」

以下では読み替えた後の問題を考えます。

解法1 貪欲法

次のような貪欲法により答えを求める事ができます。

アルゴリズム：
報酬の初期値を \(0\) とする。以下の操作を \(R\) 回繰り返す。

• \(B=(B_1,\ldots,B_N)\) の最大値を \(B_i\) とする。 報酬に \(B_i\) を加算した後、以下の通り \(B\) を変更し、長さ \(N-2\) の列になるようにする。
  • \(i=1\) のとき、\(B_1,B_2\) を\(B\) から削除する
  • \(i=N\) のとき、\(B_{N-1},B_N\) を \(B\) から削除する
  • それ以外のとき、\(B_i\) を\(B_{i-1}-B_i+B_{i+1}\) に変更し、\(B_{i-1},B_{i+1}\) を削除する

正当性の証明

$R=0$ のとき明らか。$R>0$ の場合を考える。

$i=1,N$ の場合、最適解において $B_i$ が青になることはありえないため成立。そうでないときを考える。最適解において ランプ $i-1,i,i+1$ は青赤青または赤青赤になる。（青青青、青青赤、赤青青の場合は、報酬を減らすことなく青赤青に変更することができるため）

$B$ に対して操作を行った後の列 $(B_1,\ldots,B_{i-1}-B_{i}+B_{i-1},\ldots,B_N)$ を $B'$ とすると、
「$B$ から隣接しない $R$ 要素を選ぶ方法のうち、 $B_i$ を選ぶような方法」は
「$B'$ から隣接しない $R-1$ 要素を選ぶ方法のうち、$B_{i-1}-B_{i}+B_{i+1}$ を選ばない方法」と、
「$B$ から隣接しない $R$ 要素を選ぶ方法のうち、 $B_i$ を選ばないような方法」は
「$B'$ から隣接しない $R-1$ 要素を選ぶ方法のうち、$B_{i-1}-B_{i}+B_{i+1}$ を選ぶ方法」と、それぞれ 1 対 1 に対応することが確かめられる。
したがって、最適解がどちらの場合であっても、「$B$ から隣接しない $R$ 要素を選んだときの報酬の最大値」は「$B'$ から隣接しない $R-1$ 要素を選んだときの報酬の最大値 $+B_i$」と等しいことがわかった。

このアルゴリズムは priority_queue を用いて実装することができるため、\(O(N\log N)\) で問題を解くことができます。

参考：JOI2018春合宿Day4『飴(Candies)』公式解説

解の凸性の証明

以降で述べる解法2,3では、答えが \(R\) の関数として上に凸であることを利用します。そのため、まずそのことを示します。

主張：
\(A=(A_1,\ldots,A_N)\) とし、\(f(x)\) を 「連続する \(2\) 要素を選ばないように、\(A\) からちょうど \(x\) 要素選ぶとき、選んだ要素の和の最大値」とする。このとき \(0\leq x \leq N/2\) の範囲で\(f\) は上に凸な関数である。

このことは、解法1の貪欲法において、\(x\) が増加するごとに新たに得られる報酬が単調減少することからも示せますが、ここでは解法1に依存しない証明を行います。

証明：
整数を定義域とする関数が上に凸であることを示すには 任意の \(x\) で \(f(x-1)+f(x+1)\leq 2f(x)\) が成立することを示せば十分。\(x-1,x+1\) において最適解を達成するときに選ぶ要素の index をそれぞれ \(a=(a_1,\ldots,a_{x-1})\), \(b=(b_1,\ldots,b_{x+1})\) とし、これらをマージしてソートした列を \(c=(c_1,\ldots, c_{2x})\) とする。このとき\(c\) の index が偶数だけのもの及び奇数だけのものを抜き出した列 \(c'=(c_1,c_3,\ldots,c_{2x-1})\), \(c''=(c_2,c_4,\ldots,c_{2x})\) は \(x\) 要素の選び方としてともに有効。

\(c',c''\) が有効である理由

もしそうでないならある \(i\) が存在して \(c_{i+2}-c_i=1\) となるが、このとき、\(c_i,c_{i+1},c_{i+2}\) がそれぞれ \(a,b\) どちらからきているとしても、\(a\) または\(b\) が連続する値を含んでいることになり、\(a,b\) のとり方に反する。

\(a\) を選ぶと \(f(x-1)\)、\(b\) を選ぶと \(f(x+1)\) なので、\(c'\) と \(c''\) は合わせて \(f(x-1)+f(x+1)\) であり、特に、少なくとも一方はその半分の \(\displaystyle \frac{f(x-1)+f(x+1)}{2}\) 以上となる。したがって、実際に \(x\) 個選んで和が \(\displaystyle \frac{f(x-1)+f(x+1)}{2}\) 以上となる方法を見つけることができたので、\(\displaystyle f(x)\geq \frac{f(x-1)+f(x+1)}{2}\)が言えた。

解法2 分割統治法

\(DP[L][R][k][flag]\) を区間 \([L,R)\) から \(k\) 個赤くするときの最適解とします。flagはランプ \(L,R-1\) が赤いかどうかで4通りの情報を持ちます。

\(DP[L][R][*][*]\) は \(DP[L][M][*][*]\) および \(DP[M][R][*][*]\) から求めることができるので、これらの値は分割統治法により求めることができます。その際の計算は

\[DP[L][R][k][flag1]=\max_{i+j=k} (DP[L][M][i][flag2]+DP[M][R][j][flag3])\]

のような形になります。DPテーブルは第3添字の関数として上に凸であることから、これは Concave Max Plus Convolution であり、\(0\leq k \leq K\) の範囲全ての \(k\) についてを \(O(K)\) で求めることができます。\(K=R-L\) としてよいことから、この分割統治法全体での計算量は \(O(N\log N)\) になります。

参考：JOI2018春合宿Day4『飴(Candies)』maspyさんによる解説

解法3 二分探索

\(g(x,k)=f(x)-kx\) とおきます。\(k\) を任意に固定し、\(g\) を \(x\) の関数とみたとき、\(g\) は上に凸な関数同士の和なので上に凸です。さらに、 \(\arg \max_x g(x,k)\) は \(k\) の関数として単調減少になります。（\(\max g(k,x)\) を達成する \(x\) が複数ある場合は、そのような最大の \(x\) を \(\arg \max\) とみなすものとします）

\(\arg\max\) の単調性の証明

\(k\) が大きくなった時に \(\arg \max\) が大きくならないことを示せば良いです。すなわち、任意の \(k'\geq k\) に対して、「『\(x\leq x'\) かつ \( g(k,x)\geq g(k,x')\)』 ならば \(g(k',x) \geq g(k',x')\)」を示せば十分です。

仮定の下で

\[ g(x,k')=g(x,k)-(k'-k)x\geq g(x',k)-(k'-k)x'=g(x',k')\]

となるので示せました。

\(k\) を固定したとき、\(\max_x g(x,k)\) 及び \(\arg\max_x g(x,k)\) は \(O(N)\) のDPにより容易に求めることができます。

\(g(x,k)\) は「連続するランプを赤くできず、ランプを \(1\) 個赤くするごとに \(k\) の罰金が発生するとき、\(x\) 個赤くしたときの報酬の最大値」なので、\(\max_x g(x,k)\) は「連続するランプを赤くできず、ランプを \(1\) 個赤くするごとに \(k\) の罰金が発生するとき、報酬の最大値」です。よって、連続性の条件だけに注意して

DP[i][flag]= \(i\) 番目までのランプの色を決め、ランプ \(i\) を赤に(した/しない)ときの報酬の最大値

というDPにより求まります。

したがって、\(\arg\max_x g(x,k)=R\) となる \(k\) を二分探索により求めることで、元の問題の答えは \(Rk+\max_x g(x,k)\) として求めることができます。計算量は \(O(N\log A)\) です。

(イメージ図)

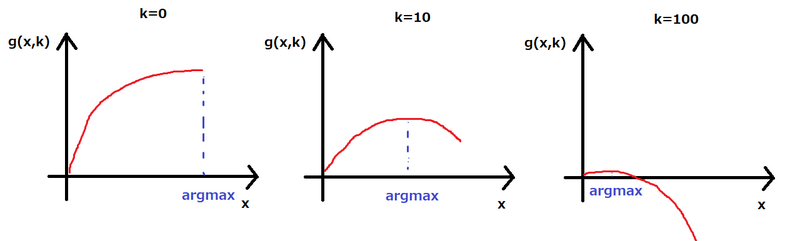
Nyaanさんによる解説 に別の可視化方法もあり、こちらの方がわかりやすいかもしれません。