We can assume \(R\leq N/2\) by flipping red and blue.

In the optimal solution, no two red lamps are adjacent to each other.

We will show that if there are consecutive red lamps, then we can increase the reward with some appropriate operations.
Take the maximum \(i\) such that Lamp \(i\) and Lamp \(i+1\) are both red. Take the minimum \(j\geq i\) such that Lamp \(j\) and Lamp \(j+1\) are both blue (or \(j = N\) if there is no such \(j\)). Then, we can flip the colors of Lamp \(i+1\) through Lamp \(j\) so that we can increase the amount of reward without changing the number of red lamps in most cases.
The only exception is when \(j=N\) and \(N\) is lighted red, in which case flipping the colors decreases the number of red lamps by one. However, we can prove that there are three consecutive blue lamps in the range of Lamp \(1\) through \(i-1\), or both Lamp \(1\) and Lamp \(2\) are blue, so by flipping such one from blue to red, we can still increase the amount of reward without changing the number of red lamps.

Therefore, the problem can be rephrased as follows.

“Given \(N\) lamps numbered \(1\) through \(N\), you will light exactly \(R\) lamps in red and the remaining in blue. You will gain a reward of \(B_i\) if you light Lamp \(i\) in red. If you are forbidden to light two adjacent lamps in red, what is the maximum sum of reward?”

Hereinafter we will consider the rephrased problem.

Solution 1: Greedy

WIP

The proof that the solution is concave

In the following Solutions 2 and 3, we will use the properties that the answer is a concave function of \(R\). We first prove that property.

Claim:
For \(A=(A_1,\ldots,A_N)\), let \(f(x)\) be “the maximum sum of \(x\) elements of \(A\) chosen so that no two adjacent elements is chosen.” Then, \(f\) is a concave function in the range \(0\leq x \leq N/2\).

Proof:
In order to prove that a function defined on integers is concave, it is sufficient to prove that \(f(x-1)+f(x+1)\leq 2f(x)\) for all \(x\). Let \(a=(a_1,\ldots,a_{x-1})\) and \(b=(b_1,\ldots,b_{x+1})\) be the indices achieving the optimal solution for \(x-1\) and \(x+1\), respectively, and let \(c=(c_1,\ldots, c_{2x})\) be a concatenation of \(a\) and \(b\), sorted. Then, a sequence consisting of even-indexed elements of \(c\), \(c'=(c_1,c_3,\ldots,c_{2x-1})\), and that of odd-indexed elements, \(c''=(c_2,c_4,\ldots,c_{2x})\), are both valid choices of \(x\) elements.

Why \(c'\) and \(c''\) are valid?

If not, then there exists \(i\) such that \(c_{i+2}-c_i=1\), but it implies that no matter which sequence (\(a\) or \(b\)) \(c_i,c_{i+1}\) and \(c_{i+2}\) originates from, either \(a\) or \(b\) contains consecutive values, which violates the rules of \(a\) and \(b\).

Combination \(a\) weighs \(f(x-1)\) and combination \(b\) weighs \(f(x+1)\), so \(c'\) and \(c''\) weighs \(f(x-1)+f(x+1)\), and especially at least one of them is no less than the half, \(\displaystyle \frac{f(x-1)+f(x+1)}{2}\). Therefore, we could actually find a combinations of \(x\) elements whose sum is at least \(\displaystyle \frac{f(x-1)+f(x+1)}{2}\), so we can see \(\displaystyle f(x)\geq \frac{f(x-1)+f(x+1)}{2}\).

Solution 2: Divide and conquer

Let \(DP[L][R][k][flag]\) be the optimal solution when lighting in red \(k\) lamps of \([L,R)\). The parameter flag can take four values depending on whether \(L\) and \(R-1\) is red.

Since \(DP[L][R][*][*]\) can be obtained from \(DP[L][M][*][*]\) and \(DP[M][R][*][*]\), these values can be obtained by divide-and-conquer. This can be found through the relations

\[DP[L][R][k][flag1]=\max_{i+j=k} (DP[L][M][i][flag2]+DP[M][R][j][flag3]).\]

Since the DP table is concave over the third index, this is Concave Max Plus Convolution, so the value for all \(k\) in the range \(0\leq k \leq K\) in a total of \(O(K)\) time. Since we may assume \(K=R-L\), the total time complexity over all this divide-and-conquer is \(O(N\log N)\).

See also: Editorial by maspy of JOI 2018 Spring Camp Day 4 “Candies” (in Japanese)

Solution 3: Binary search

Let \(g(x,k)=f(x)-kx\). For some fixed \(k\), if we regard \(g\) as a function of \(x\), then \(g\) is a sum of concave functions and therefore concave. Moreover, \(\arg \max_x g(x,k)\) is monotonically decreasing as a function of \(k\). (If there are multiple \(x\) achieving \(\max g(k,x)\), we regard maximum such \(x\) as the \(\arg \max\))

Proof of monotonicity of \(\arg\max\)

It is sufficient to prove that increasing \(k\) does not increase \(\arg \max\). Precisely, it is sufficient to prove that “if ‘\(x\leq x'\) and \( g(k,x)\geq g(k,x')\)’, then \(g(k',x) \geq g(k',x')\).

Under the assumption,

\[ g(x,k')=g(x,k)-(k'-k)x\geq g(x',k)-(k'-k)x'=g(x',k')\]

so it has been proved.

For a fixed \(k\), \(\max_x g(x,k)\) and \(\arg\max_x g(x,k)\) can be found in an \(O(N)\) DP.

\(g(x,k)\) is “the maximum amount of reward for lighting \(x\) lamps in red, when no consecutive lamps can be lighted red and a fine of \(k\) is imposed for each of lamps lighted in red,” so \(\max_x g(x,k)\) is “the maximum amount of reward when no consecutive lamps can be lighted red and a fine of \(k\) is imposed for each of lamps lighted in red.” Therefore, with the consecutiveness constraints in mind, we can find it with a DP of

DP[i][flag]= the maximum amount of reward obtained from the first \(i\) lamps when Lamp is (or is not) lighted in red.

Therefore, by finding \(k\) such that \(\arg\max_x g(x,k)=R\) by binary search, the answer for the original problem can be found as \(Rk+\max_x g(x,k)\). The time complexity is \(O(N\log A)\).

(Illustration)

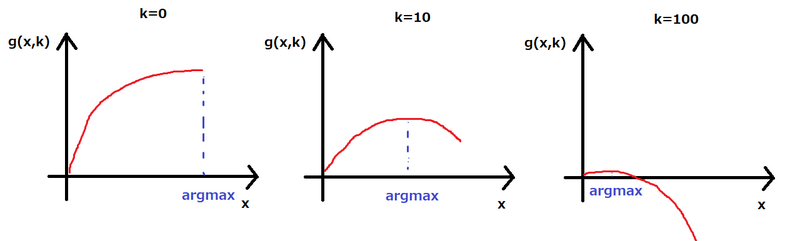
There is another visualization in the Editorial by Nyaan, which may be easier to understand.