H - Red and Blue Lamps Editorial
by  Nyaan
Nyaan
この解説はユーザー解説のような位置づけで、内容としては解法の1つである Alien DP の「お気持ち」を説明します。
この問題自体の解説は kyopro_friends さんによる公式解説 の方を参照ください。また、Alien DP に関する数理的な説明は noshi91 さんによる Kyopro Encyclopedia of Algorithms の記事 をご参照ください。
さて、この問題は次のように言い換えられます。
\(N\) 個のボールのうち \(R\) 個を隣り合わないように黒く塗る。 ボール \(i\) を黒く塗ると \(A_{i-1} + A_{i}\) のスコアを得る。 スコアの最大値は?
\(N \leq 2 \times 10^5, R \leq \left\lfloor \frac{N}{2} \right\rfloor\)
以下では \(N = 11, A = (3,1,4,1,5,9,2,6,5,3)\) の場合を例に挙げて説明します。このとき、\(R = x\) としたときの答えを \(f(x)\) と表すと、 \(x = 0,1,\dots,5\) のときの \(f(x)\) の値、および \(f(x)\) の隣接する値同士を直線で結んだグラフは実験すると以下のように求まります。
| x | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| f(x) | 0 | 14 | 25 | 30 | 35 | 39 |
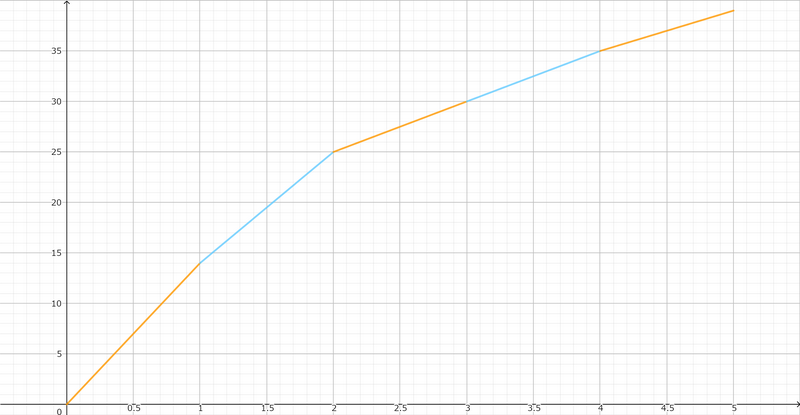
グラフを見るとわかると通り、 \(f(x)\) のグラフは上に凸な関数になります。これは一般の \(N, A\) に対して証明できます。(他の方に教えて頂きました)
- 略証 : \(f(k-1) + f(k+1) \leq 2 f(k)\) を証明すればよい。 \(x=k-1,k+1\) の場合に最適に選んだときのボールのindex の集合をそれぞれ \((a_1,\dots,a_{k-1}), (b_1,\dots, b_{k+1})\) とおき、その二つをマージしてソートした列を \((c_1,\dots,c_{2k})\) とする。 このとき \((c_1,c_3,\dots,c_{2k-1}), (c_2,c_4,\dots,c_{2k})\) はともに valid な \(k\) 個の選び方を示しており、かつ少なくとも一方のスコアは \(\frac{f(k-1) + f(k+1)}{2}\) 以上である。
求めたいのは \(f(R)\) の値ですが、個数と位置を持った DP テーブルを埋めていく方法では \(\mathrm{\Omega}(N^2)\) かかってしまいます。なぜならば、 DP テーブル自体のマス目の個数が \(\mathrm{O}(N^2)\) 個なので、 愚直な DP を行う限りは計算量の下界は \(N^2\) オーダーになってしまうからです。
ここで突然ですが発想を大きく転換します。まずは次の問題を解いてみましょう。
\(N\) 個のボールのうち いくつかのボール を隣り合わないように黒く塗る。 ボール \(i\) を黒く塗ると \(A_{i-1} + A_{i}\) のスコアを得る。 また、ボールを \(1\) 個塗るごとにスコアが \(8\) 点減る。 スコアの最大値は? また、そのときの塗った個数の最大値は?
この問題は \(\mathrm{O}(N)\) の DP で解くことができます。そして、この問題の答えは明らかに
\[\max_{x=0,1,\dots,5} f(x) - 8x\]
で、先ほどの例の場合はスコアの最大値は \(x = 2\) のとき \(9\) になります。 この式をグラフに落とし込んでみましょう。高校数学の知識を思い出すと、上の条件を満たす \(x\) はグラフ上では \(y = f(x)\) と \(y = 8x + m\) の最も上側の交点として表せるのでした。よって視覚的には以下のように表されます。

このように \(1\) 個選んだときのコストを \(C\) と固定すると、求める答えは \(y = f(x)\) と \(y = Cx + m\) のグラフ上での交点の \(x\) 座標に言い換えることができます。この性質を利用すると愚直に DP テーブルを埋めなくても \(f(R)\) を求めることができる、というのがこれから説明する Alien DP の本質的な部分です。
さて、もとの問題に戻りましょう。まず、\(T = f(R) - f(R - 1)\) と置きましょう。 \(C\) を固定して DP を行ったとき、グラフ上に傾き \(C\) の直線を落として考えると \(T,C,R\) の関係は以下のようになることがわかります。
- \(C \leq T\) のとき : 選んだ個数の最大値は \(R\) 以上である
- \(C \gt T\) のとき : 選んだ個数の最大値は \(R\) 未満である
よって \(C\) の値で二分探索を行うことで \(T\) の値を求めることができます。これは言い換えると、最適解が \(K\) 個になる \(C\) の値を求めることができるというわけなので、\(T\) の値が求めたあとは \(C = T\) とおいて DP したときのスコアに \(TR\) を足したものが元の問題の答えになる、というわけです。
このように \(R\) 個選ぶ という制約を \(1\) 個選ぶごとに \(C\) 円の罰金 と言い換えて問題を解き、 \(C\) の値で二分探索をすることで適切な \(C\) の値を求め、最後に \(f(R)\) を求める、というのが Alien DP の「お気持ち」です。
実装例は次の通りです。 提出
いくつか注意点を付記しておきます。
- 境界値周りを意識して実装しないと、個数がちょうど \(R\) 個になる \(C\) が存在しない場合にバグを埋め込む可能性があります。
たとえば上の例の場合、 \(f(3)-f(2)\) と \(f(4) - f(3)\) はともに \(5\) になっているので、 最適解がちょうど \(3\) 個塗るような \(C\) は存在しません。このようなケースではスコアのみを優先順位として DP を行うと正しい \(T\) の値が求まらない場合があります。これは、たとえば DP 内で「スコアが同じ場合はより塗った個数が大きい方を採用する」という実装を行うことで解決できます。 - 二分探索に実数を利用すると \(N,A\) が大きいケースで正しい答えが求まりません。 Alien DP を扱った資料の多くでは二分探索を実数で行っていますが、この問題の場合は答えの最大値が \(2 \times 10^{14}\) と大きいため要求される精度が非常に高く、 DP 内で異符号の加算を行う影響もあり正確に \(C\) を計算することができません。
この問題では傾きが整数なのを利用して \(C\) を整数上で二分探索を行うことで解決できます。実数の場合は前述の境界値周りの問題を考慮せずに処理しても(微小な誤差が発生することを無視すれば)正答が求まりますが、整数の場合は丁寧に実装する必要性が生まれることに注意してください。
posted:
last update:
