 /
/ 
実行時間制限: 2 sec / メモリ制限: 256 MiB
配点 : 300 点
問題文
自己ループと二重辺を含まない N 頂点 M 辺の重み無し無向グラフが与えられます。
i (1≦i≦M) 番目の辺は頂点 a_i と頂点 b_i を結びます。
ここで、自己ループは a_i = b_i (1≦i≦M) となる辺のことを表します。
また、二重辺は a_i=a_j かつ b_i=b_j (1≦i<j≦M) となる辺のことを表します。
頂点 1 を始点として、全ての頂点を1度だけ訪れるパスは何通りありますか。
ただし、パスの始点と終点の頂点も訪れたものとみなします。
例として、図1のような無向グラフが与えられたとします。
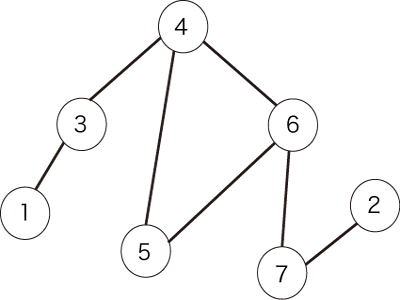
図1:無向グラフの例
このとき、図2で表されるパスは条件を満たします。
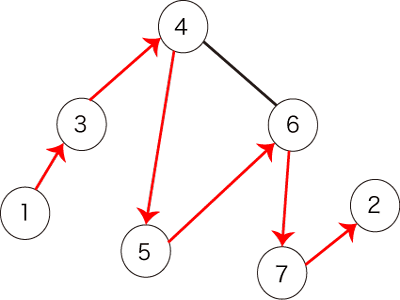
図2:条件を満たすパスの例
しかし、図3で表されるパスは条件を満たしません。全ての頂点を訪れていないからです。
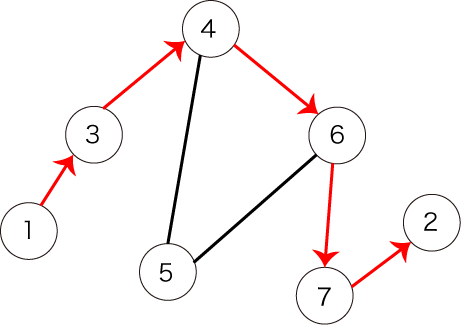
図3:条件を満たさないパスの例1
また、図4で表されるパスも条件を満たしません。始点が頂点 1 ではないからです。
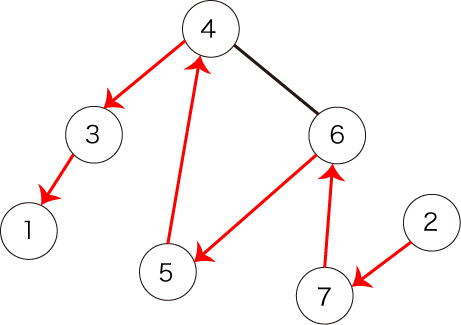
図4:条件を満たさないパスの例2
制約
- 2≦N≦8
- 0≦M≦N(N-1)/2
- 1≦a_i<b_i≦N
- 与えられるグラフは自己ループと二重辺を含まない。
入力
入力は以下の形式で標準入力から与えられる。
N M a_1 b_1 a_2 b_2 : a_M b_M
出力
問題文の条件を満たすパスが何通りあるか出力せよ。
入力例 1
3 3 1 2 1 3 2 3
出力例 1
2
与えられるグラフは以下の図で表されます。
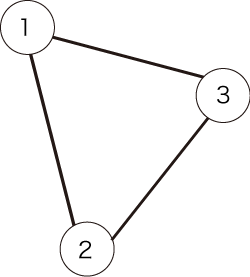
条件を満たすパスは以下の 2 通りです。
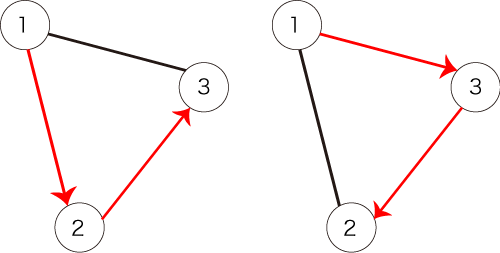
入力例 2
7 7 1 3 2 7 3 4 4 5 4 6 5 6 6 7
出力例 2
1
このテストケースは問題文の例と同じです。
Score : 300 points
Problem Statement
You are given an undirected unweighted graph with N vertices and M edges that contains neither self-loops nor double edges.
Here, a self-loop is an edge where a_i = b_i (1≤i≤M), and double edges are two edges where (a_i,b_i)=(a_j,b_j) or (a_i,b_i)=(b_j,a_j) (1≤i<j≤M).
How many different paths start from vertex 1 and visit all the vertices exactly once?
Here, the endpoints of a path are considered visited.
For example, let us assume that the following undirected graph shown in Figure 1 is given.

Figure 1: an example of an undirected graph
The following path shown in Figure 2 satisfies the condition.

Figure 2: an example of a path that satisfies the condition
However, the following path shown in Figure 3 does not satisfy the condition, because it does not visit all the vertices.

Figure 3: an example of a path that does not satisfy the condition
Neither the following path shown in Figure 4, because it does not start from vertex 1.

Figure 4: another example of a path that does not satisfy the condition
Constraints
- 2≦N≦8
- 0≦M≦N(N-1)/2
- 1≦a_i<b_i≦N
- The given graph contains neither self-loops nor double edges.
Input
The input is given from Standard Input in the following format:
N M a_1 b_1 a_2 b_2 : a_M b_M
Output
Print the number of the different paths that start from vertex 1 and visit all the vertices exactly once.
Sample Input 1
3 3 1 2 1 3 2 3
Sample Output 1
2
The given graph is shown in the following figure:

The following two paths satisfy the condition:

Sample Input 2
7 7 1 3 2 7 3 4 4 5 4 6 5 6 6 7
Sample Output 2
1
This test case is the same as the one described in the problem statement.