 /
/ 
Time Limit: 2 sec / Memory Limit: 256 MiB
問題文
高橋君はタテ、ヨコともに 10^8 マスずつある方眼紙を使って以下の問題を解くことにしました。
「一番左下のマスから開始して、右もしくは上に1マス移動するという操作を繰り返して、各マスにたどり着く方法の個数を 1,000,000,007 で割った余りを求めよ。」
高橋君は動的計画法が好きなので、この問題が動的計画法を使って解けるということにすぐ気づきました。
具体的には
- 最も左の列もしくは最も下の行に属する全てのマスに 1 を書き込む。
- まだ整数が書き込まれていないマスについて、左のマスにも下のマスにも整数が書かれていたら、その 2 マスの和を1,000,000,007 で割った余りをそのマスに書き込む。
- 整数が書かれていないマスがなくなるまで操作2を繰り返す。
というアルゴリズムによって、答えを求めることが出来ます。
高橋君は上記のアルゴリズムですべてのマスに「左下からたどり着く方法の個数を 1,000,000,007 で割った余り」を書き込みました。
できあがった方眼紙の左下の一部は下図のようになります。
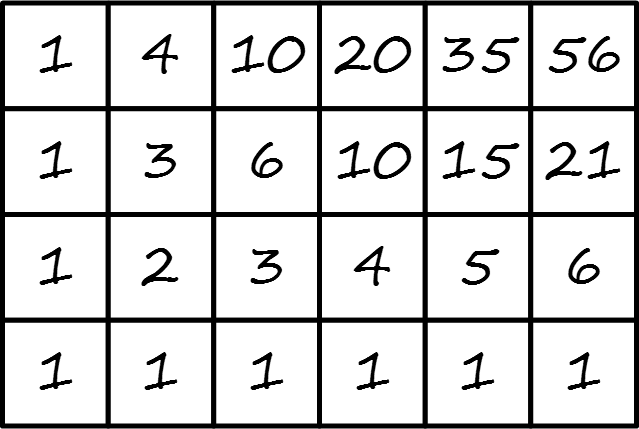
しかし書き込み終わったあと、達成感のために舞い上がってしまい、方眼紙の一部を破いてしまいました。
高橋君の手元には、あるマスと、その上のマスと右のマスの部分のみが書かれている方眼紙の欠片があります。
高橋君はこの欠片を元の位置に戻そうと思ったのですが、方眼紙が大きすぎるので、どこに置けばいいのかわかりません。
欠片の情報から、この欠片が元々の方眼紙の左から何マス、下から何マスの位置にあったのか求めてください。
つまり、左からxマス、下からyマスのマスのことを (x, y) と書くとして、(r, c)、(r, c + 1)、(r + 1, c)のマスに書かれている整数が与えられるので、 r と c を求めてください。
なお、一番左下のマスは (0, 0) です。
入力
入力は以下の形式で標準入力から与えられる。
A B C
- 1 行目には (r, c) のマスに書かれている整数 A(0 ≦ A < 1,000,000,007) が与えられる。
- 2 行目には (r, c + 1) のマスに書かれている整数 B(0 ≦ B < 1,000,000,007) が与えられる。
- 3 行目には (r + 1, c) のマスに書かれている整数 C(0 ≦ C < 1,000,000,007) が与えられる。
- 0 ≦ r, c < 99,999,999となるような答えが存在するような A, B, C が与えられる。
出力
欠片が元々あった位置を表す 2 つの整数 r(0 ≦ r < 99,999,999) と c(0 ≦ c < 99,999,999) を空白区切りで出力せよ。 答えとして考えられる r, c が複数あった場合はそのなかで r が最小のものを出力せよ。 それでも答えが 1 つに定まらない場合は、rが最小のもののなかで c が最小のものを出力せよ。 出力の末尾には改行を入れること。
入力例1
15 35 21
出力例1
4 2
高橋君の手元にある欠片は下図のようなものです。

元はあった位置としては下図の位置があてはまります。
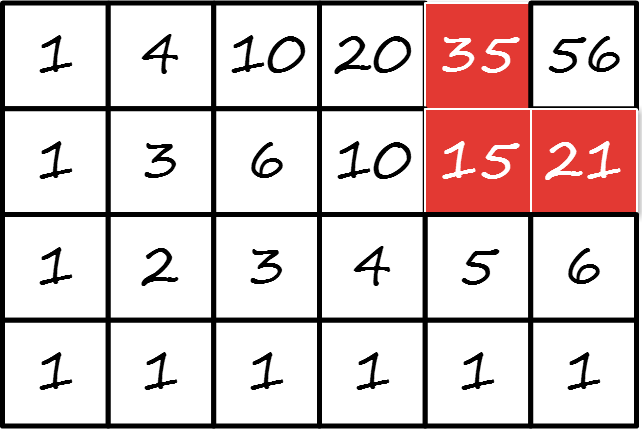
入力例2
126 252 210
出力例2
5 4
入力例3
144949225 545897619 393065978
出力例3
314159 365358