 /
/ 
実行時間制限: 0 msec / メモリ制限: 0 KiB
キーポイント
- プログラムを実行するときには処理内容に応じた実行時間がかかる
- コンピュータの記憶領域(メモリ)は有限であり、プログラムで変数を使用した分だけメモリを消費する
- プログラムの実行時間・メモリ使用量が入力に応じてどのように変化するかを見積もったものを、それぞれ時間計算量・空間計算量という
- 計算量の表記方法としてオーダー記法が存在する
アルゴリズム
ある処理を行うプログラムを作成するときに、どのような計算を行っていくかという計算手順のことをアルゴリズムといいます。
例えば、1 から 100 まで整数の総和を計算するプログラムを考えます。1 + 2 + 3 + \cdots + 99 + 100 と順番に足していくというのは 1 つのアルゴリズムです。これをアルゴリズム A とします。一方、\frac{100 \times (1 + 100)}{2} という式を用いて計算するというのもアルゴリズムです。これをアルゴリズム B とします。
この例のように、プログラムを作成するにあたって複数のアルゴリズムが考えられることがあります。そのような場合には、どちらのアルゴリズムを用いるのかを選ぶことになります。
コンピュータでの計算は一回一回僅かとはいえ時間が掛かるので、計算回数が多くなるほど実行時間が長くなります。より計算回数が少ないアルゴリズムを選択することによって、高速に動作するプログラムを作成できます。
上の例でのアルゴリズム A は 99 回の足し算が必要ですが、アルゴリズム B では足し算・掛け算・割り算の計 3 回の計算で結果を求めることができます。99 回の計算が必要なアルゴリズム A と、3 回の計算が必要なアルゴリズム B、というように必要な計算の回数で大まかな性能を見積もることができます。
アルゴリズムの性能を比較する方法は色々ありますが、1 つの指標として計算量という考え方があります。
計算量
プログラムは入力に対して計算を行い、結果を出力します。このときに必要な計算時間や記憶領域の大きさが入力に対してどれくらい変化するか、ということを示す指標を計算量といいます。
計算量には時間計算量と空間計算量があります。単に計算量という場合、時間計算量を指すことが多いです。
時間計算量
「プログラムの計算のステップ数が入力に対してどのように変化するか」という指標を時間計算量といいます。計算のステップ数とは、四則演算や数値の比較などの単純な演算の回数です。
空間計算量
「プログラムが使用するメモリの量が入力に対してどのように変化するか」という指標を空間計算量といいます。メモリとはコンピュータの記憶領域のことを指し、変数を使用した分だけメモリを消費します。また、文字列や配列などは内部の要素数等に応じてメモリを消費します。
計算量の例
次のプログラムは 1 から N までの総和 (1 + 2 + 3 + \cdots + N) をループを用いて計算するものです。
N = int(input())
s = 0
for i in range(1, N + 1):
s += i
print(s)
このプログラムでは for 文で N 回の繰り返し処理を行っているので、計算ステップ数は入力の N の大小に応じて変わります。N 回の繰り返しを行うので、計算ステップ数はおおよそ N 回になります。このときの時間計算量は次で紹介するオーダー記法を用いて O(N) と表します。
このプログラムで使用している変数は、入力の N の大小に関わらず N と s と i の 3 つです。 このときの空間計算量はオーダー記法を用いて O(1) と表します。
オーダー記法
厳密な計算ステップ数や必要な記憶領域の量は実装に用いるプログラミング言語や実装方法などによって異なるため、計算にかかる時間や記憶領域を厳密に見積もるのは非常に困難です。
このため、時間計算量や空間計算量の表現としてオーダー記法 O(\cdot) がよく用いられます。
例えば、3N^2 + 7N + 4 という式は、オーダー記法を用いて 3N^2 + 7N + 4 = O(N^2) などと表すことができます。これは、N が大きくなると、定数や詳細な係数を無視した場合にこの式が N^2 と同じ、またはそれよりも緩やかに増加することを意味します。
以下の手順によってオーダー記法による表記を得ることができます。
- ステップ 1: 係数を省略する。ただし定数については 1 とする。
- ステップ 2: N を大きくしたときに一番影響が大きい項を取り出し、O(\text{項}) と書く。
- 補足:N^2 + N + 1 という式の場合、「N^2」「N」「1」 それぞれを項といいます。
「一番影響が大きい項」というのは、基本的には N を大きくしていったときに「大きくなるスピードが最も速い項」と考えることができます。例えば N と N^2 を比較すると以下の表のようになるので、N^2 の方がより影響が大きいといえます。
| N | N^2 | |
|---|---|---|
| N = 1 | 1 | 1 |
| N = 10 | 10 | 100 |
| N = 100 | 100 | 10{,}000 |
| N = 1{,}000 | 1{,}000 | 1{,}000{,}000 |
3N^2 + 7N + 4 という式をオーダー記法で表す場合の手順は以下の通りです。
- ステップ 1: 係数を省略して N^2 + N + 1 とする。
- ステップ 2: N^2 + N + 1 で一番影響の大きい項は N^2 なので O(N^2) とする。
同じように 2N + 10 なら O(N) となります。
例題
次の式をそれぞれオーダー記法で表してください。
- N + 100
- 10N + N^3
- 3 + 5
- 2^N + N^2
- 補足:2^N = \underbrace{2 \times 2 \times \cdots \times 2}_{N \text{個}} であり、例えば 2^3 = 2 \times 2 \times 2 = 8 です。
答え
2^N と N^2 の比較は以下の通りです。クリックで答えを開く
2^N
N^2
N = 1
2
1
N = 3
8
9
N = 10
1{,}024
100
N = 30
1{,}073{,}741{,}824(約 10 億)
900
計算量(オーダー記法)の求め方
計算量を求めるには、計算ステップ数について式で表す必要があります。
次のプログラムについて、計算量がどうなるかを考えてみましょう。
N = int(input())
s = 0
for i in range(1, N + 1):
for j in range(1, N + 1):
s += i * j
for i in range(1, N + 1):
s += i
for i in range(1, N + 1):
s += i * i
print(s)
1 つの二重ループと 2 つの一重ループがあるので、計算ステップはおおよそ N^2 + 2N ほどになります。よってこのプログラムの時間計算量は O(N^2) です。
このように、簡単なアルゴリズムであれば厳密な式を求めなくても「N 回の繰り返し処理があるから O(N)」や「1 から N+1 まで回す二重ループがあるから O(N^2)」などと見積もることができます。
例
いくつかの計算量オーダーについて、具体的なプログラムの例を挙げます。
O(1)
次のプログラムは、1 から N までの総和を公式を使って計算するものです。このプログラムの計算量は O(1) です。
""" 1 から N までの総和を公式を使って計算するプログラム 計算量:O(1) """ N = int(input()) s = N * (N + 1) // 2 print(s)
入力
10
実行結果
55
O(N)
次のプログラムは、要素数 N の配列の中に含まれる偶数の個数を数えるものです。このプログラムの計算量は O(N) です。
"""
要素数 N の配列の中に含まれる偶数の個数を数えるプログラム
計算量:O(N)
"""
N = int(input())
a = list(map(int, input().split()))
cnt = 0
for x in a:
if x % 2 == 0:
cnt += 1
print(cnt)
入力
5 1 4 2 5 9
実行結果
2
O(N^2)
次のプログラムは、九九の要領で N \times N マスを埋めるものです。このプログラムの計算量は O(N^2) です。
"""
九九の要領で N × N マスを埋めるプログラム
計算量:O(N^2)
"""
N = int(input())
table = [[0 for j in range(N)] for i in range(N)]
for i in range(N):
for j in range(N):
table[i][j] = (i + 1) * (j + 1) # N × N 回実行される
for row in table:
print(*row)
入力
9
実行結果
1 2 3 4 5 6 7 8 9 2 4 6 8 10 12 14 16 18 3 6 9 12 15 18 21 24 27 4 8 12 16 20 24 28 32 36 5 10 15 20 25 30 35 40 45 6 12 18 24 30 36 42 48 54 7 14 21 28 35 42 49 56 63 8 16 24 32 40 48 56 64 72 9 18 27 36 45 54 63 72 81
N \times N 要素の二次元配列を使っているので空間計算量も O(N^2) となります。
なお、上のプログラムは以下のように書くこともできます。以下の書き方でも時間計算量、空間計算量ともに元の書き方と変わらず O(N^2) となります。
"""
九九の要領で N × N マスを埋めるプログラム
計算量:O(N^2)
"""
N = int(input())
table = [[(i + 1) * (j + 1) for j in range(N)] for i in range(N)]
for row in table:
print(*row)
O(\log N)
まずはじめに簡単に \log について説明をします。
\log_{x} N という式は「x を何乗したら N になるか」を表します。例えば、2^4 = 16 なので、\log_{2} 16 = 4 です。
以下の図を見てください。長さ 8 の棒を長さが 1 になるまで半分に切る(2 で割る)ことを繰り返したときに切る回数は \log_{2} 8 = 3 回です。

このように計算量に出てくる \log は「半分にする回数」を表すことが多いです。
\log N は N に対して非常に小さくなるので、計算量の中に O(\log N) が出てきた場合でも実行時間にそこまで影響しないことが多いです。
オーダー記法では \log の底( \log_{2} 8 の _2 の部分)は省略して書かれることが多いです。
なぜなら、\log の底の違いは定数倍の違いだけとみなすことができ、オーダー記法では定数倍は省略するからです。
次のプログラムは N が 2 で何回割り切れるかを数えるものです。このプログラムの計算量は O(\log N) です。
上に挙げたイメージと同じような処理を行うプログラムなので、ループする回数が最大でも \log_{2} N 回になることが分かります。
"""
N が 2 で何回割り切れるかを数えるプログラム
計算量:O(log N)
"""
N = int(input())
cnt = 0
while N % 2 == 0:
cnt += 1
N //= 2
print(cnt)
計算量のおおまかな大小
主な計算量の大まかな大小は以下のようになります。
O(1) \lt O(\log N) \lt O(N) \lt O(N \log N) \lt O(N^2) \lt O(2^N)
時間計算量なら O(1) 側ほど高速に計算可能で、O(2^N) 側ほど時間がかかります。
これらの関係をグラフに示すと以下のようになります。
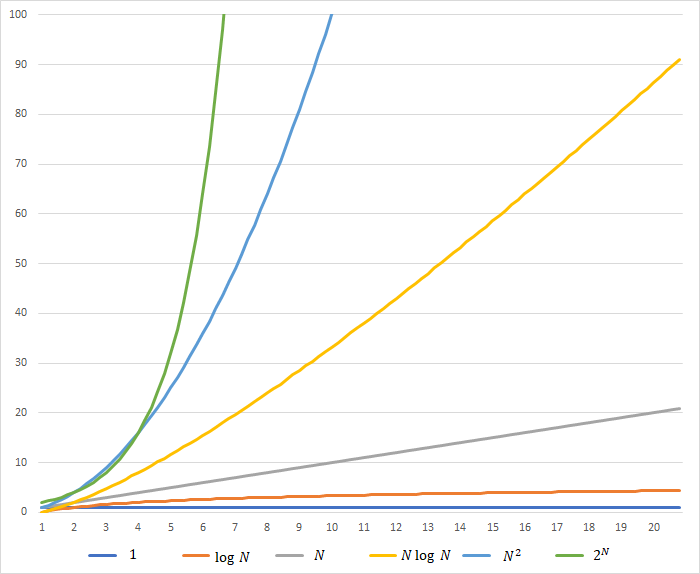
入力 N と実行時間のおおよその感覚との対応を次の表に示します。
| N | O(1) | O(\log N) | O(N) | O(N \log N) | O(N^2) | O(2^N) |
|---|---|---|---|---|---|---|
| 1 | 一瞬 | 一瞬 | 一瞬 | 一瞬 | 一瞬 | 一瞬 |
| 10 | 一瞬 | 一瞬 | 一瞬 | 一瞬 | 一瞬 | 一瞬 |
| 1{,}000 | 一瞬 | 一瞬 | 一瞬 | 一瞬 | 0.01 秒くらい | 地球爆発 |
| 10^6 | 一瞬 | 一瞬 | 0.01 秒くらい | 0.2 秒くらい | 3 時間くらい | 地球爆発 |
| 10^8 | 一瞬 | 一瞬 | 1 秒くらい | 30 秒くらい | 3 年くらい | 地球爆発 |
| 10^{16} | 一瞬 | 一瞬 | 3 年くらい | 170 年くらい | 地球爆発 | 地球爆発 |
1 秒くらいで計算が終わるようなプログラムを作りたいときは、入力の大きさの上限を見積もった上で 1 秒以内に収まるような計算量のアルゴリズムを選択する必要があります。
例えば、N = 10^6 くらいまでの入力で 1 秒以内に計算を終えるプログラムを作成するのであれば、O(N^2) のアルゴリズムでは間に合わない可能性が高いので、O(N) や O(N \log N) のアルゴリズムを用いて実装する必要があります。
AtCoder の問題では実行時間制約が 2 秒 ~ 5 秒くらいであることが多いです。コンテストに参加する人は、1 秒あたり 10^8 回くらいの計算ができることを覚えておきましょう。
複数の入力がある場合のオーダー記法
プログラムの入力が複数ある場合もオーダー記法で計算量を表すことができます。この場合それぞれの変数を残して書きます。例えば、2 つの入力 N と M を受け取る場合は O(N+M), O(NM), O((N+M)\log N) などのように書きます。
また、例えば N^2 M + NM + NM^2 という計算ステップ数になった場合は、計算量に影響する入力がひとつのときと同様に影響が一番大きくなりうる項のみを残すので O(N^2 M + NM^2) となります。
どの項を残すのかが分からなくても計算量の比較さえできればよいので問題ありません。複数の入力が計算量に影響することがあるということは頭に入れておきましょう。
細かい話
オーダー記法の落とし穴
計算量をオーダー記法で表記すると比較しやすくなりますが、オーダー記法は大まかな比較しかできない点に注意する必要があります。
オーダー記法では影響の一番大きな項のみを残して係数を省略して書きます。これによって、例えば計算ステップ数が 20N になるアルゴリズムと 2N になるアルゴリズムを比較しようとしたときに、実際には 10 倍もの差があるのに、オーダー記法ではどちらも O(N) となってしまいます。
同様の理由で、O(N) のアルゴリズム A と O(N \log N) のアルゴリズム B を比較するときに、計算量上はアルゴリズム A の方が高速でも、実際に動かしてみるとアルゴリズム B の方が高速だったということも起こり得ます。
正確に比較する必要がある場合は、実際に時間を計測して比較する必要があります。
組み込み関数の計算量
1.12.組み込み関数 で紹介した関数のうち、リストや文字列などを受け取る関数について、計算量は以下のようになります。
| 関数 | 計算量(引数のリスト等の長さを N とする) |
|---|---|
len |
O(1)(以下に補足あり) |
sum |
O(N) |
sorted |
O(N \log N) |
len 関数についてlen 関数は、リストや文字列などの多くの組み込み型に対しては O(1) で動作します。これらの型では要素数が事前に管理されているため、単純な参照で済みます。しかし、カスタムクラスで __len__ メソッドを独自に定義している場合、その計算量は定義内容に依存します。
累乗計算を行う pow 関数についてpow(base, exp, mod) 関数では、指定方法によって計算量が変わります。
mod 引数を指定する場合(例: pow(2, 10, 100))は、モジュロ演算を使うため(mod が非常に大きくなければ)計算量は O(\log(\mathrm{exp})) になります。mod 引数を指定しない場合(例: pow(2, 1000))は、大きな数の掛け算が必要になるため多倍長整数の乗算アルゴリズムに依存した計算量になります。
\log の性質
- O(\log 5N) \rightarrow O(\log N) (\log 5N = \log 5 + \log N なので)
- O(\log NM) \rightarrow O(\log N + \log M) (\log NM = \log N + \log M なので)
- どちらで書いてもよいですが、大きさを考えるときにこの関係を知っていると見積もりやすいかもしれません。
- O(\log N^2) \rightarrow O(\log N) (\log (N^2) = 2 \log N なので)
- O(\log 2^N) \rightarrow O(N) (\log (2^N) = N \log 2 なので)
問題
リンク先の問題を解いてください。