問題文

1 個の入力ファイルにつき T 個のテストケースが与えられる．各テストケースで次のようなグラフ G が与えられるので，以下の問に答えよ．

G は N 頂点 M 辺の無向単純グラフである．頂点には 1, 2, \ldots, N と番号が付いている．i 番目 (1 \le i \le M) の辺は頂点 A_i と頂点 B_i を結ぶ．

G の各頂点と各辺を金色と銀色のいずれかで塗る方法を考える (そのような塗り方は 2^{N+M} 通りある)．芸術的な塗り方とは，以下の条件をすべて満たす塗り方のこととする：

• 任意の金色の辺に対し，それが結ぶ頂点のうち少なくとも 1 つは金色である．
• 任意の銀色の頂点に対し，それに接続する辺のうち少なくとも 1 つは銀色である．

芸術的な塗り方の個数を 2 で割った余りを求めよ．

制約

• 1 \le T \le 100．
• 0 \le N \le 2024．
• 0 \le M \le 2024．
• 1 \le A_i < B_i \le N   (1 \le i \le M)．
• 1 \le i < j \le M のとき，(A_i, B_i) \ne (A_j, B_j)．

入力例 1

1
3 2
1 2
1 3

出力例 1

1

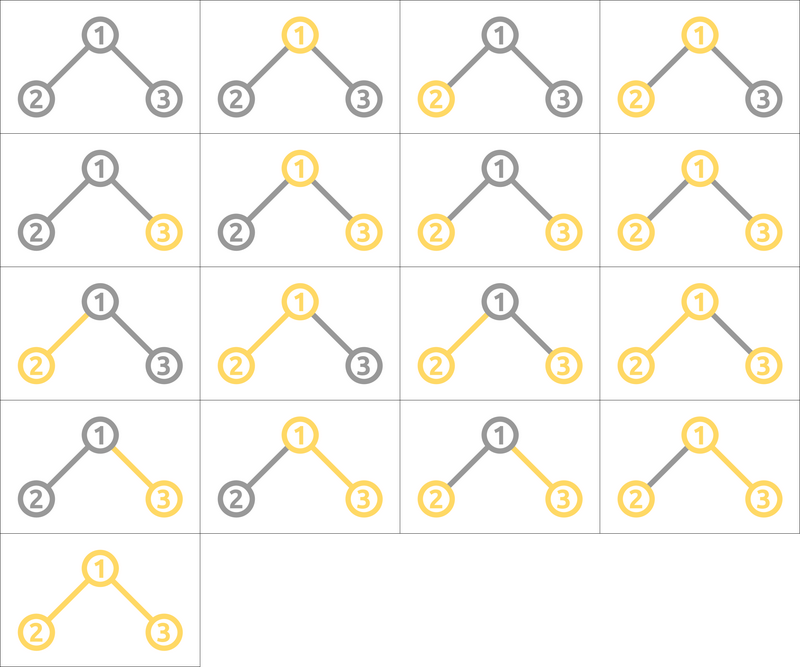
1 個目のテストケースでは，芸術的な塗り方は以下の図の 17 通りである．