(より詳しい解説は後日ブログで公開します)

\(M\) が \(2\) 冪のとき解は存在しません．証明：すべての辺の重みを割り切る最大の \(2\) 冪を \(2^e\) とします．\(n \ge 2\) かつ \(1 \le c_i < M\) なので \(2^e < M\) で，\(M\) は \(2\) 冪なので \(2^{e+1} | M\) です．頂点 \(1\) からの距離が \(2^{e+1}\) の倍数かどうかで頂点を黒白で塗ると，\(2^e\) の奇数倍の重みの辺が存在するので，黒頂点も白頂点も存在します．すると，頂点 \(1, \ldots, n\) を順に辿るとどこかで色が変わりますが，黒頂点と白頂点の距離は \(2^{e+1}\) の倍数ではないので，条件を満たしません．

\(M\) が \(2\) 冪でないときは解が存在します．\(M > 1\) が奇数のときが解ければあとは全体定数倍すればよいです．以下，具体例で説明します．辺の重みは \({} \bmod M\) で書きます．

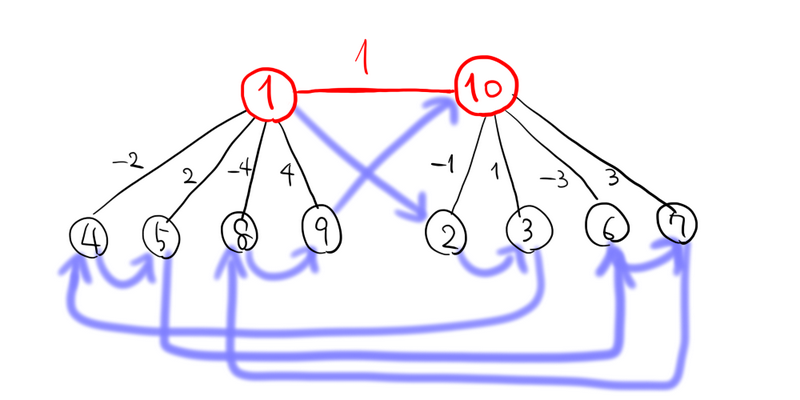
下図 (\(M = 5\) の例) のようにすると \(2M\) 頂点でできます．まず頂点 \(1, n\) を結ぶ重み \(1\) の辺を用意して，葉を付けていきます．まず頂点 \(n\) に重み \(-1\) で葉を付けられます．その後以下の \(2\) 種類の操作ができます：

• 今いる側に葉を付ける．重みは \(x \mapsto -x\) になる．
• 反対側に葉を付ける．重みは \(x \mapsto -(x+1)\) になる．

これらを繰り返すと頂点 \(1\) に重み \(M-1\) で葉を付けられるので完成です．

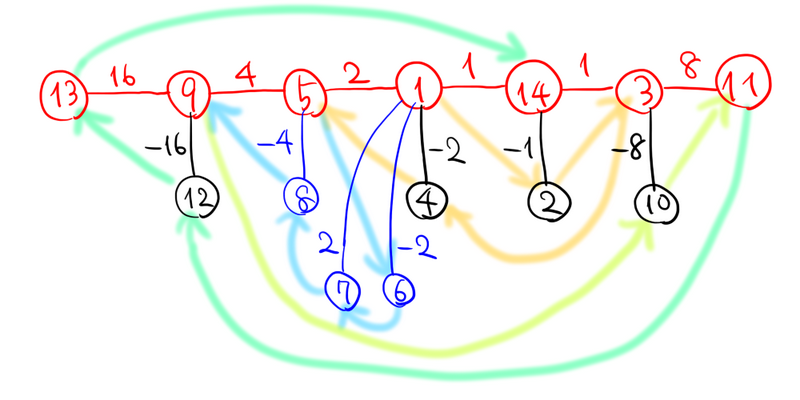
下図 (\(M = 23\) の例) のようにすると約 \(4 \log_2(M)\) 頂点以下でできます．赤い部分は頂点 \(1, n, 3\) から左右に広がっていくパスで，\(M\) の立っているビットが左側に，立っていないビットが右側に配置されます．パスの端にいるとき，以下の \(2\) 種類の操作ができます：

• \(2\) 頂点使って，パスを反対側に伸ばす．
• \(4\) 頂点使って，パスをいまいる側に伸ばす．図の青色で書かれた部分．

これらを適切な順序で組み合わせて，最後にパスの左端から頂点 \(n\) に移動したとき合計 \(M\) になるようにできます．