以下，レベル \(i\) のフラクタルを生成する際に中央に配置される三角形を下向きの三角形と，そうでない三角形を上向きの三角形と呼ぶことにします．

このとき，上向きの三角形と隣り合っている三角形は必ず下向きであり，また逆も然りです．したがって，Alice は必ず上向きと下向きの三角形を交互に訪れていくことになります．

上向きの三角形は，全てレベル \(1\) です．また，下向きの三角形については，レベル \(l\) \((1 \leq l \leq L)\) の三角形が \(3^{L-l}\) 個あります．

よって，下向きの三角形のレベルの総和を最大化する問題に帰着させればよいことがわかります．

ここで，下向きの三角形のレベルごとの訪れられる回数について，以下の事実が成り立ちます：

• レベル \(L-l\) の三角形は，最大でも \(2^{l}\) 個までしか訪れることができない．

上記の事実を，数学的帰納法で示します．

\(l = 0\) のときは，レベル \(L\) の三角形の個数が \(1=2^0\) 個であることから成り立ちます．

\(l = 0, 1, \dots, k-1\) について成立していると仮定した場合に，\(l = k\) の場合を考えます．このとき，レベル \(L-k\) の三角形を訪れる代わりに，それが属しているレベル \(L-k+1\) のフラクタルを訪れることとして考えます．

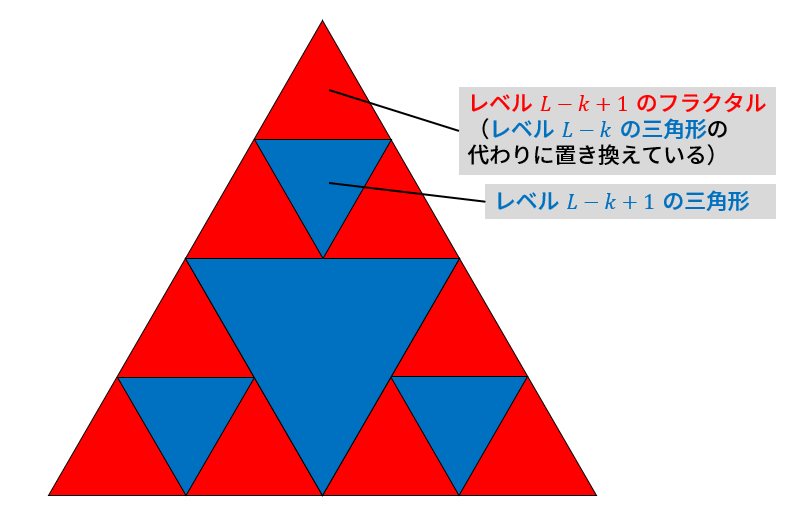
このとき，先述の上向き・下向きの三角形の議論と同様にして，レベル \(L-k+1\) のフラクタルは，レベル \(L-k+1\) 以上の三角形と交互に訪れなければならない（すなわち，レベル \(L-k+1\) 以上の三角形を訪れることなく，レベル \(L-k+1\) のフラクタルを \(2\) 個以上訪れることはできない）ことがわかります．帰納法の仮定により，訪れられるレベル \(L-k+1\) 以上の三角形の個数は，\(1 + 2 + \dots + 2^{k-1} = 2^{k}-1\) 個です．このことより，レベル \(L-k\) の三角形は最大でも \(2^k\) 個しか訪れられないことがわかります．

これをもとにして，下向きの三角形のレベルの総和の最大化問題を考えます．

実は，下向きの三角形については，レベルごとの個数制約のもとで貪欲に選択した場合，それらを訪れる移動方法が実際に必ず存在することがわかります．これは，三角形のレベルごとにレベル \(L\) のフラクタルの外辺のうちの \(1\) 辺に沿って，一方向的に訪れるものを選択する，という方法によって可能です．このようにして選択された三角形を，辺に沿った順番に訪れることを考えると，連続した順番のどの \(2\) つの三角形に対しても，その \(2\) つの三角形と辺で接する上向きの三角形が存在しており，実際に移動が実現可能であることがわかります．

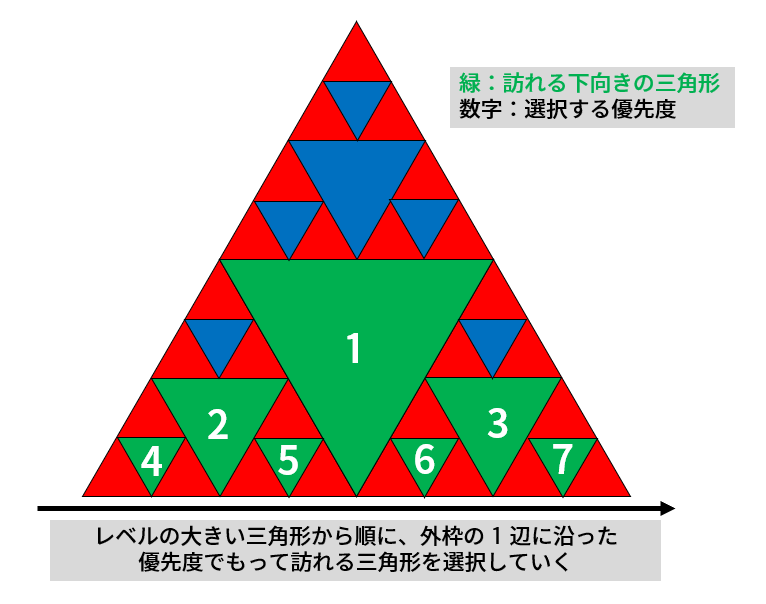
レベルごとに，訪れられる三角形の個数は指数的に増加していくため，訪れる下向きの三角形のレベルの種類数は \(O(\log K)\) 種類となります．これにより，同じレベルの三角形をまとめる形でシミュレーションを行うことにより，答えを求めることができます．

\(L\) が小さくて \(K\) が大きい場合など，可能な移動回数が \(K\) 回に満たないことがある点に注意してください．