帰着された整数計画問題を再掲します．

\[ \mathrm{maximize} \sum_{i=0}^{M-1}x_i\ \ \mathrm{subject\ to}\ 0\leq x_i\leq B_i\land x_{i-1}+x_i\leq C_i\]

（整数計画問題の制約）

• \(0\leq B_i\leq \min(C_i,C_{i+1})\)
• \(0\leq C_i\)
• \(\sum C=N\)

これの答えが各クエリに対して高速に求められれば良いです．この整数計画問題を最小カットに言い換えて解きます．

N個のバケツ と似ているので，こちらの解説スライドも参考にしてください．

[1] \(M\) が偶数のとき

整数計画問題の答えはは以下のグラフ \(G\) の最大流（最小カット）に等しくなります．（\(M=6\) の場合）

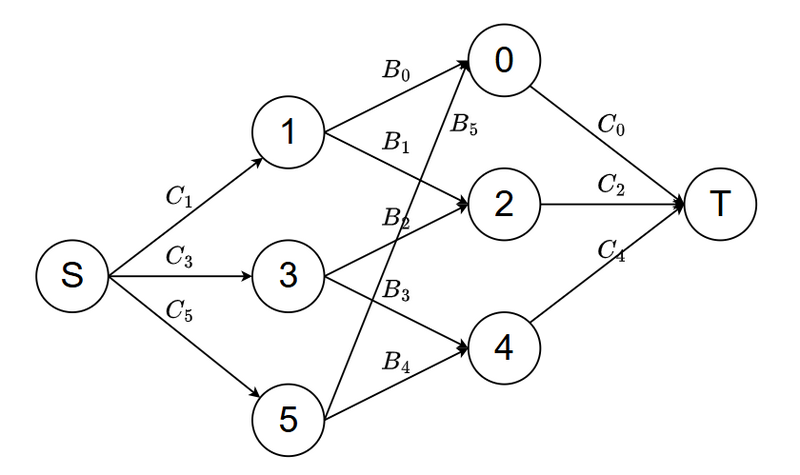
すなわち，頂点 \(0,1,\ldots,M-1\) に S または T を書き込んだときの，辺の両端に書かれている文字が異なるような辺すべての流量上限の総和の最小値が答えになります．

\(\mathrm{dp}[l][r][s_l][s_r]\) を次のように定義します

• 頂点集合 \(\{S,T,l,l+1,\ldots,r\}\) の \(G\) の誘導部分グラフ（ただし頂点 \(M-1\) から頂点 \(0\) の辺が含まれる場合はそれを除く） において，頂点 \(l\) に文字 \(s_l\)，頂点 \(r\) に文字 \(s_r\) を書きこむときの最小カット．

\(\mathrm{dp}[l][m-1][s_l][s_{m-1}]\) と \(\mathrm{dp}[m][r][s_m][s_r]\) が分かれば \(\mathrm{dp}[l][r][s_l][s_r]\) を求めることができるので，この dp はセグ木に乗せることができます．

\(\mathrm{dp}[0][M-1][\ast][\ast]\) が求められれば簡単な計算によって整数計画問題の答えが求められます．

[2] \(M\) が奇数のとき

\(M\) が奇数のときは偶数のときのようなグラフでは表現が難しいです．\(B_{M-1}\) の条件を除くとグラフで表現できます．（\(M=5\) の場合）

ここで，整数計画問題における \(x_{M-1}\) の値を固定すると，そのときの \(\sum x_i\) の最大値は以下のグラフにおける最小カットと \(x_{M-1}\) の和になります．

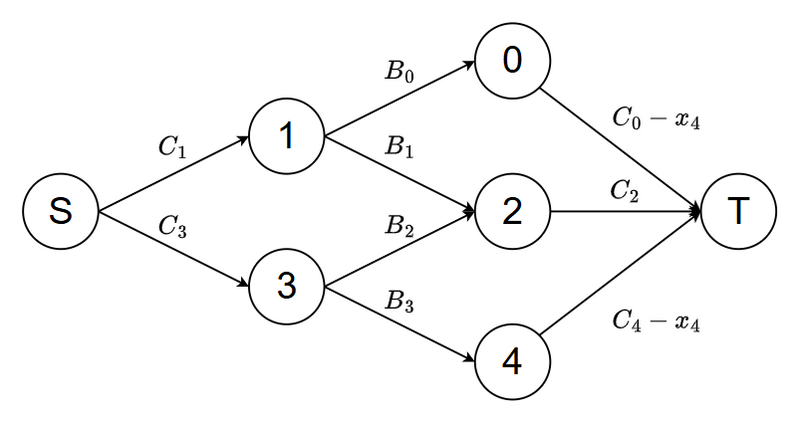
\(x_{M-1}\) を変動させたときに，最小カットで切る辺の集合としてありうるものは \(3\) 通りしかなく，それぞれの場合の最小カットは \(x_{M-1}\) の一次関数で表されることを利用することで答えを求めることができます．（詳しい内容はN個のバケツと同じなのでそちらを参照してください ．）

計算量は \(O((N+Q)\log(N+Q)+M+Q\log M)\) です．

実装例