浮動小数点数を用いて凸包を求める際の注意点について述べます。 以下、直線の交点の座標は (分数の形を経由することで) ある程度正確に表現できているものとします。

ここでは一般的と思われる次のアルゴリズムを考えます。

using Real = T; // T は浮動小数点数の型
using Point = complex<Real>;
const Real EPS; // 誤差を吸収するための微小な量

// 右手系での外積 (cross product) : a×b=|a||b|sinΘ
Real cross(Point a, Point b) {
  return a.real() * b.imag() - a.imag() * b.real();
}

// 点群 p の凸包の頂点を返す
vector<Point> ConvexHull(vector<Point> p) {
  int n = p.size();
  if(n <= 2) return p;
  sort(all(p), [&](Point a, Point b) {
    return !equal(real(a), real(b)) ? real(a) < real(b) : imag(a) < imag(b);
  });
  int sz = 0;
  Poly CH(2 * n);
  rep(i, n) {
    // cross の正確な値が 0 以下なら CH から pop する
    while((sz > 1 && cross(CH[sz - 1] - CH[sz - 2], p[i] - CH[sz - 2]) < EPS))
      sz--;
    CH[sz] = p[i];
    sz++;
  }
  int t = sz;
  for(int i = n - 2; i >= 0; i--) {
    while((sz > t && cross(CH[sz - 1] - CH[sz - 2], p[i] - CH[sz - 2]) < EPS))
      sz--;
    CH[sz] = p[i];
    sz++;
  }
  CH.resize(sz - 1);
  return CH;
}

浮動小数点数を用いて凸包を計算する場合、次の点が問題となります。

• 定数 EPS が小さすぎると、正確な外積 (cross) は 0 以下で本来 pop されるべき頂点が、 EPS より大きいと判定されて残り続けてしまう
• EPS が大きすぎると、正確な外積 (cross) は 0 より大きく凸包の頂点になるべき点が、EPS 以下と判定されて pop されてしまう

特に前者の問題は深刻で、次のような図が凸包とみなされ、面積が過小に計算される可能性があります。(図は CDE の外積の計算で誤差が発生した場合)

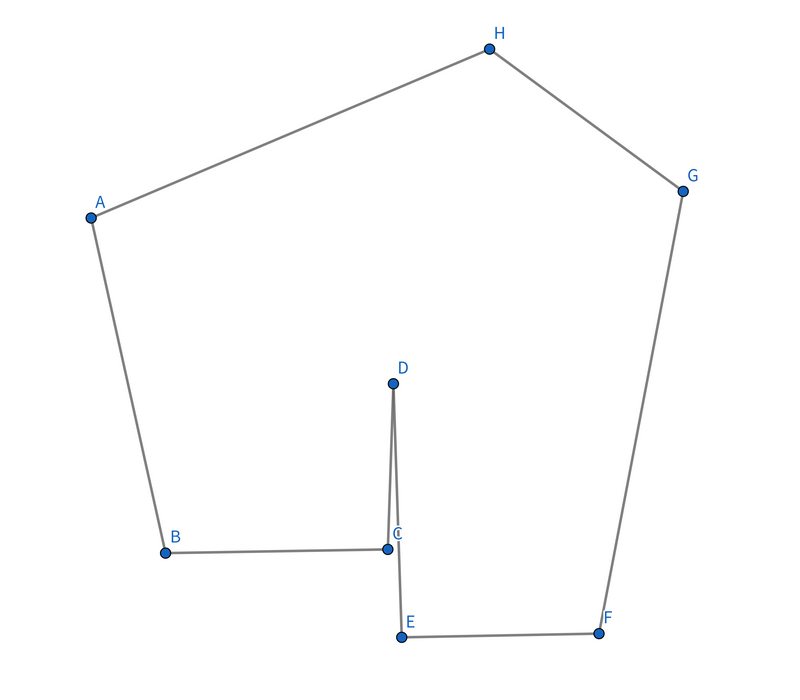
では、定数 EPS や型 T として何を選ぶべきでしょうか。

正確な外積が \(C > 0\) である頂点を pop した場合、最終的な面積が高々 \(C / 2\) だけ小さくなります。そのため、 \(N \times \text{EPS} \ll 10^{-5}\) となるように設定するのが良さそうです。

また、交点の座標としてありうる最大値を \(M = O(\max{(A, B, C)}^2)\) 、型 T での相対誤差を \(\epsilon\) とします。 このとき、cross の計算において発生しうる誤差は \(O(M^2 \epsilon)\) であり、 \(M^2 \epsilon \ll \text{EPS}\) を満たすべきです。

以上より、 EPS として \(10^{-9}\) 程度を選び、 \(\epsilon \ll 10^{-21}\) を満たすよう 128bit の浮動小数点数を利用することで、正解を得やすくなると考えられます。