以下では順列と、順列を写像ととらえたものを同一視しています。また、二つの順列 \(P,Q\) に対して \(PQ\) で合成を表します。
すなわち、\((PQ)_i=P_{Q_i}\) です。

条件の言い換え

一旦転倒数に関する条件を忘れて

• \(PQ=X\)
• \(QP=Y\)
  

を満たす \(P,Q\) が存在するような順列 \(X,Y\) を考えます。
\(2\) つの式を整理することで、

• \(P=XQ^{-1}\)
• \(QXQ^{-1}=Y\)

となります。 ここで、第二式を観察すると、 \(Y\) は \(Q_i\) を \(Q_{X_i}\) に送る順列です。よって、\(X\) と \(Y\) をサイクルに分解した時にサイクルのサイズからなる多重集合が等しい必要があることが分かります。

逆に、サイクルのサイズの多重集合が等しければ、サイクルごとに値の対応を考えることで \(QXQ^{-1}=Y\) なる \(Q\) を構成することができます。

この対応の直感的理解については以下の図を参考にしてください。

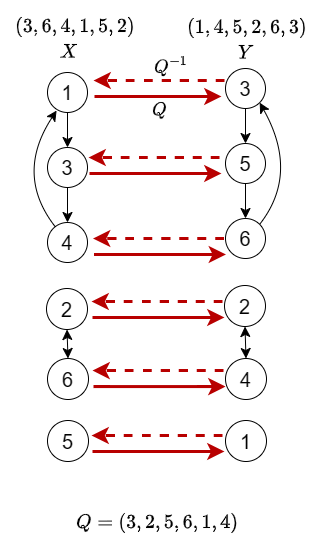
また、群論的背景やこの対応を具体的に式で表したものは ユーザー解説 をご覧ください。

以上より、この問題はサイクル分解のふるまいと転倒数で特徴づけられた二つの順列を扱う問題へと言い換えられました。

構築(アイデア編)

前節の議論から、以下を満たす正整数 \(k\) 及び正整数列 \(C=(c_1,c_2,\dots,c_k)\) を探す必要があります。

• \(\sum_{i=1}^{k}c_i=N\)
• サイクル分解した時に各サイクルのサイズからなる多重集合が \(\{c_1,c_2,\dots,c_k\}\) となるような順列 \(X,Y\) であって、転倒数がそれぞれ \(A,B\) となるものが存在する。

本解説では探索方針の一例として、存在性が変化しない程度に強い条件を \(C\) に課し、その条件下を探す方針をとります。　
具体的には \(C\) に、

• \(\max C\le 3\)
• \(\max C=3\implies \min C>1\land \#\{i\mid c_i=3\}=1\)

という条件を課すことにします。
すなわち、 \(C\) として

• \(0\) 個以上の \(1\) と \(0\) 個以上の \(2\) からなる集合
• \(0\) 個以上の \(2\) と丁度 \(1\) 個の \(3\) からなる集合

のいずれかに絞ります。以降この条件を条件(\(\star\)) と書きます。

ここからは、まずこれらの \(C\) について転倒数の取りうる値を調べます。
そしてその後に、 \(C\) に追加した条件(\(\star\))によって存在性が変化しない事を示します。

\(0\) 個以上の \(1\) と \(0\) 個以上の \(2\) からなる集合のパターン

\(C\) が \(1\) を \(a\) 個と \(2\) を \(b\) 個含むとします。(すなわち \(N=a+2b\) です。)
\(b=0\) の時明らかに転倒数として取る値は \(0\) のみです。以下は \(b>0\) を考えます。

結論から述べると、\(n\) が転倒数としてとりうることと、 \(b\le n\le b(2N-2b-1)\) かつ \(b\equiv n\pmod 2\) は同値です。

証明:
転倒数の下界として \(b\) があり、これは明らかに達成可能です。
また、上界として \(2b(b-1)+2b(N-2b)+b=b(2N-2b-1)\) があります。
左辺の \(3\) 項はそれぞれ

1. サイズ \(2\) の相異なるサイクル間で生じる転倒数の上界
2. サイズ \(2\) のサイクルとサイズ \(1\) のサイクル間で生じる転倒数の上界
3. サイズ \(2\) のサイクル内で生じる転倒数の上界

を表しています。

そしてこの上界もまた、順列を \((N,N-1,\dots,N-b+1,b+1,b+2,\dots,N-b,b,b-1,\dots,1)\) とすれば達成可能です。

さらに、以下のステップを実行することによって \(b\le n\le b(2N-2b-1)\) かつ \(b\equiv n\pmod 2\) を満たす全ての \(n\) が転倒数として現れます。

1. \(P=(2,1,4,3,\dots,2b,2b-1,2b+1,2b+2,\dots,N)\) とする。
2. \(P=(N,N-1,\dots,N-b+1,b+1,b+2,\dots,N-b,b,b-1,\dots,1)\) となるまで \(3.\sim 5.\) を繰り返す。
3. \(P=(L_1,R_1)(L_2,R_2)\dots(L_b,R_b)\) と互換の積(参考: ユーザー解説)で表す。
4. \(R_i+1=R_j\) なる \(j\) が存在せず、 \(R_i<N\) なる \(i\) をひとつ選ぶ。ここでは一般性を失わず \(i=1\) を選べたとする。
5. \(R_1+1=L_j\) なる \(j\) が存在する場合、一般性を失わず \(j=2\) として、\(P=(L_1,L_2)(R_1,R_2)(L_3,R_3)\dots(L_b,R_b)\) に置き換える。
   • \(R_1+1=L_j\) なる \(j\) が存在しない場合、\(P=(L_1,R_1+1)(L_2,R_2)(L_3,R_3)\dots(L_b,R_b)\) に置き換える。

実際、\(2.\) の形以外の順列について \(4.\) での \(i\) が存在すること及び、 \(5.\) の操作で転倒数が丁度 \(2\) 増加することが確認できます。

\(0\) 個以上の \(2\) と丁度 \(1\) 個の \(3\) からなる集合

\(C\) が \(2\) が \(b\) 個と \(3\) が \(1\) 個からなるとします。(すなわち \(N=2b+3\) です。)

こちらも結論から述べると、\(n\) が転倒数としてとりうることと、 \(b+2\le n\le 2b^2+5b+2\) かつ \(b\equiv n\pmod 2\) は同値です。
証明に関しては先のケースとほぼ同様のため省略します。

これで条件(\(\star\))を課した \(C\) について転倒数の取りうる値が分かったため、\(C\) に条件(\(\star\))を課したことによる存在性の不変を示します。

\(C=(1,\dots,1,c_1,c_2,\dots,c_n)\) \((2\le c_1\le\dots\le c_n)\) に対し、\(a(C)\) を \(1\) の個数とし、\(m(C),M(C)\) を以下の通りに定めます。

\[\begin{aligned}m(C)=\sum_{i=1}^{n}(c_i-1)\end{aligned}\\\\ M(C)=\left\{\sum_{i=2}^{n}\sum_{j=1}^{i-1}c_ic_j\right\}+\left\{\sum_{i=1}^{n}a(C)c_i\right\}+\left\{\sum_{i=1}^{n}\left\lceil\frac{1}{2}(c_i-1)^2\right\rceil\right\} \]

\(m(C),M(C)\) はそれぞれ転倒数として取りうる値の下界、上界を与えています。

$M(C)$ についての補足

$M(C)$ の $3$ つの項については、先ほど同様それぞれ

1. サイズ $2$ 以上の異なるサイクル間で生じる転倒数の上界
2. サイズ $2$ 以上のサイクルとサイズ $1$ のサイクル間で生じる転倒数の上界
3. サイズ $2$ 以上のサイクル内で生じる転倒数の上界

を表しています。

このうち非自明なのは $3$ つ目の、サイズが $k$ のサイクル内での転倒数が　$f(k)\coloneqq\left\lceil\dfrac{(k-1)^2}{2}\right\rceil$ で抑えられる点です。 これを帰納法によって証明します。

まず、 $k=1,2$ の時は直接計算をすることで確かめることができます。

$k\ge 3$ の場合を考えます。

考える順列を $P=(p_1,p_2,\dots,p_k)$ とします。 $p_1\gt p_2\gt\dots\gt p_k$ とすると、$P=(k,k-1,\dots,1)$ であるため、 $P$ がサイズ $k$ のサイクルであることと矛盾します。

そうでない時、ある $i$ が存在して $p_i\lt p_{i+1}$ です。

$P'=(p_1,p_2,\dots,p_{i-1},p_{i+1},p_{i},p_{i+2},\dots,p_{k})$ とします。すなわち、 $P$ から $p_i$ と $p_{i+1}$ を入れ替えた順列とします。

この時、 $P'$ は

• 丁度二つのサイクルからなる順列
• 転倒数は $P$ の転倒数 $+1$

となります。

$P'$ のサイクルの各サイズを $u,v$ とします。帰納法の過程から、 $$\mathrm{inv}(P)+1\le f(u)+f(v)+uv$$ です。

ここで、 $$\begin{aligned} f(u+v)&=\left\lceil\dfrac{(u+v-1)^2}{2}\right\rceil\\ &=\left\lceil\dfrac{u^2+v^2+2uv-2u-2v+1}{2}\right\rceil\\ &=\left\lceil\dfrac{u^2+v^2-2u-2v+3}{2}\right\rceil+uv-1\\ &=\left\lceil\dfrac{(u-1)^2+(v-1)^2+1}{2}\right\rceil+uv-1\\ &\ge\left\lceil\dfrac{(u-1)^2}{2}\right\rceil+\left\lceil\dfrac{(v-1)^2}{2}\right\rceil+uv-1\\ \end{aligned}$$ であるため、先の不等式と併せて目当ての不等式 $\mathrm{inv}(P)\le f(u+v)=f(k)$ を示せました。

既に、\(C\) が条件(\(\star\))を満たす場合に \(m(C)\le n\le M(C),m(C)\equiv n\pmod{2}\) なる \(n\) が全て転倒数として達成可能であることを示しているため、ここで示すべきは、一般の \(C\) について、列 \((C_0=C,C_1,\dots,C_k)\) であって以下の条件を満たすものの存在です。

• \(C_k\) は条件(\(\star\)) を満たす。
• \(i=1,2,\dots,k\) について、 \(m(C_{i-1})\equiv m(C_i)\pmod2\)
• \(i=1,2,\dots,k\) について、 \(m(C_{i-1})\ge m(C_i)\)
• \(i=1,2,\dots,k\) について、 \(M(C_{i-1})\le M(C_i)\)

これは以下のように \(C\) が条件\((\star)\) を満たさない場合に適切な \(C'\) を拵えることで構築できます。

\(a(C)>0\) の時

\(C=(\overbrace{1,\dots,1,1}^{a(C)\text{ 個}},c_1,c_2,\dots,c_n)\) とします。
一般性を失わず \(2\le c_1\le c_2\le\dots\le c_n\) とします。
\(c_n\le 2\) ならすでに条件(\(\star\))を満たしているため良いです。
そうでない時、\(C'=(\overbrace{1,\dots,1,1}^{a(C)-1\text{ 個}},2,c_1,\dots,c_{n-1},c_{n}-1)\) とします。 ただし、\(1\) の個数を一つ減らして総和が不変となるようにします。すると計算によって

• \(m(C)\equiv m(C')\pmod2\)
• \(m(C)\ge m(C')\)
• \(M(C)\le M(C')\)

が確認できます。

$M(C)\le M(C')$ の計算

$\begin{aligned} M(C')&=\left(\sum_{i=2}^{n-1}\sum_{j=1}^{i-1}c_ic_j\right)+(c_n-1)\left(\sum_{i=1}^{n-1}c_i\right)+2\left(\sum_{i=1}^{n-1}c_i\right)+2(c_n-1)\\ &+\left(\sum_{i=1}^{n}(a(C)-1)c_i\right)+(a(C)-1)(c_n-1)+(a(C)-1)\cdot2\\ &+\left(\sum_{i=1}^{n-1}\left\lceil\dfrac{(c_i-1)^2}{2}\right\rceil\right)+\left\lceil\dfrac{(c_n-2)^2}{2}\right\rceil+1\\ &=\left(\sum_{i=2}^{n}\sum_{j=1}^{i-1}c_ic_j\right)+\left(\sum_{i=1}^{n}a(C)c_i\right)+\left(\sum_{i=1}^{n}\left\lceil\dfrac{(c_i-1)^2}{2}\right\rceil\right)\\ &+2(c_n-1)-c_n-a(C)+1+2(a(C)-1)\\ &+\left\lceil\dfrac{(c_n-2)^2}{2}\right\rceil-\left\lceil\dfrac{(c_n-1)^2}{2}\right\rceil+1\\ &=M(C)+c_n+a(C)-2+\left\lceil\dfrac{(c_n-2)^2}{2}\right\rceil-\left\lceil\dfrac{(c_n-1)^2}{2}\right\rceil\\ &=M(C)+a(C)-1+\left\lceil\dfrac{(c_n-1)^2+1}{2}\right\rceil-\left\lceil\dfrac{(c_n-1)^2}{2}\right\rceil\\ &\ge M(C) \end{aligned}$

\(a(C)=0\) かつ \(\max(C)>3\) の時

\(C=(c_1,c_2,\dots,c_n)\) とします。
一般性を失わず \(2\le c_1\le c_2\le\dots\le c_n\) とします。
\(C'=(1,1,c_1,\dots,c_{n-1},c_{n}-2)\) とします。 すると再度簡単な計算によって

• \(m(C)\equiv m(C')\pmod2\)
• \(m(C)\ge m(C')\)
• \(M(C)\le M(C')\)

が確認できます。

$M(C)\le M(C')$ の計算

$\begin{aligned} M(C')&=\left(\sum_{i=2}^{n-1}\sum_{j=1}^{i-1}c_ic_j\right)+(c_n-2)\left(\sum_{j=1}^{n-1}c_j\right)\\ &+2\left(\sum_{j=1}^{n-1}c_j\right)+2(c_n-2)\\ &+\left(\sum_{i=1}^{n-1}\left\lceil\dfrac{(c_i-1)^2}{2}\right\rceil\right)+\left\lceil\dfrac{(c_n-3)^2}{2}\right\rceil\\ &=\left(\sum_{i=2}^{n}\sum_{j=1}^{i-1}c_ic_j\right)+\left(\sum_{i=1}^{n}\left\lceil\dfrac{(c_i-1)^2}{2}\right\rceil\right)\\ &+2c_n-4+\left\lceil\dfrac{(c_n-3)^2}{2}\right\rceil-\left\lceil\dfrac{(c_n-1)^2}{2}\right\rceil\\ &=M(C)+\left\lceil\dfrac{(c_n-1)^2}{2}\right\rceil-\left\lceil\dfrac{(c_n-1)^2}{2}\right\rceil\\ &=M(C) \end{aligned}$

\(a(C)=0\) かつ \(\max(C)=3\) の時

\(C=(c_1,c_2,\dots,c_n)\) とします。
一般性を失わず \(2\le c_1\le c_2\le\dots\le c_n\) とします。
\(c_{n-1}=2\) の場合すでに条件(\(\star\))を満たしているため良いです。

そうでない時、\(C'=(c_1,\dots,c_{n-2},1,1,2,2)\) とします。 すると三度計算によって

• \(m(C)\equiv m(C')\pmod2\)
• \(m(C)\ge m(C')\)
• \(M(C)\le M(C')\)

が確認できます。

$M(C)\le M(C')$ の計算

$C$ が $b$ 個の $2$ と $c$ 個の $3$ からなるとします。 この時、 $C'$ は $2$ 個の $1$, $b+2$ 個の $2$, $c-2$ 個の $3$ からなります。 $$\begin{aligned} M(C')&=6(b+2)(c-2)+2(b+2)(b+1)+\dfrac{9}{2}(c-2)(c-3)\\ &+4(b+2)+6(c-2)\\ &+(b+2)+2(c-2)\\ &=6bc+2b^2+\dfrac{9}{2}c^2-b-\dfrac{5}{2}c+1\\ &=6bc+2b(b-1)+\dfrac{9}{2}c(c-1)+b+2c+1\\ &=M(C)+1\\ &\ge M(C) \end{aligned}$$

以上のケースで全ての \(C\) のパターンが尽くされており、さらに \(C\) の最大値か最大値の個数は真に減少するため有限の列で条件\((\star)\)まで到達します。

構築(実装編)

以上の議論によって条件(\(\star\))

• \(\max C\le 3\)
• \(\max C=3\implies \min C>1\land \#\{i\mid c_i=3\}=1\)

を課して良いことが確認できました。

それでは条件\((\star)\)の元で

• \(\sum_{i=1}^{k}c_i=N\)
• サイクル分解した時に各サイクルのサイズからなる多重集合が \(\{c_1,c_2,\dots,c_k\}\) となるような順列 \(X,Y\) であって、転倒数がそれぞれ \(A,B\) となるものが存在する。

なる \(C\) の探索及び順列の構築をしましょう。

まず、条件(\(\star\))を満たす \(C\) は \(O(N)\) 個のみであるため全て試すことができます。
さらに、転倒数の存在性も \(C\) 中の \(1,2,3\) の個数のみから \(O(1)\) で判定出来るため、順列の存在・非存在も高速に判定できます。

存在が分かった後は、転倒数として取りうる値の計算時に用いたアルゴリズムによって順列を構築できます。但し、全てを愚直に行うとステップ数が \(\Theta(N^2)\) 回となるため、例えば同じ \(R_i\) を選び続けるステップをまとめて処理をするなどの工夫が必要です。

以上で得られた順列を、条件の言い換え章で述べた復元処理をすることで(存在すれば)所望の順列を得ることができました。