良い数列 \(A\) は，次のように考えることができます．

• \(N\) 頂点の完全グラフにおいて，頂点 \(A_1\) から順に一筆書きをして，すべての辺を一度以上通るものを考える．このとき，\(i\) 番目に訪れた頂点を \(A_i\) とする．

一般に，重複を許さずに一筆書きできる条件は，次数が奇数の頂点（奇点）が \(0\) 個または \(2\) 個のときです（オイラーの定理）．また，奇点の個数が \(0\) 個のときは，一筆書きの始点は任意の頂点にすることが可能であり，終点は始点と一致します．一方，奇点の個数が \(2\) 個のときは，一筆書きの始点は奇点のいずれかになり，終点は始点でない奇点になります．

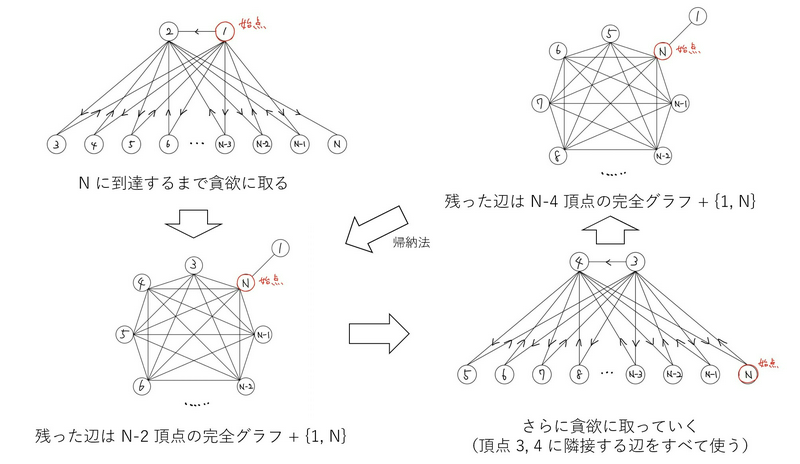
\(N\) が奇数のとき

完全グラフの任意の頂点の次数は偶数なので，重複を許さずに一筆書き可能です．よって，\(M=N(N-1)/2+1\) が最小です． 辞書順最小の構成方法について，対称性より \(A_1=1\) としてよいです．このとき終点も \(A_M=1\) になることに注意しながら貪欲に構成することができます（貪欲法の正当性は数学的帰納法によって証明できます）．再帰的に解くことも可能です．

帰納法の概略

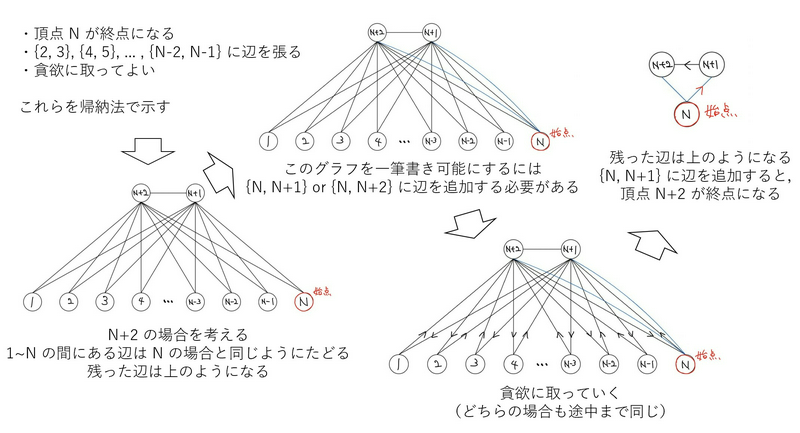
\(N\) が偶数のとき

完全グラフの任意の頂点の次数は奇数なので，完全グラフに \((N-2)/2\) 個の（多重）辺を追加することで，重複を許さずに一筆書き可能です．よって，\(M=N(N-1)/2+(N-2)/2+1=N^2/2\) が最小です． 辞書順最小の構成方法について，対称性より \(A_1=1\) としてよいです．このとき貪欲に構成することができます（貪欲法の正当性は数学的帰納法によって証明できます）．なお，追加する辺は \(\{2,3\}, \{4,5\}, \{6,7\}, \ldots\) としてよいことも数学的帰納法によって証明できます．再帰的に解くことも可能です．

帰納法の概略

\(N\) が小さい場合の答えを以下に示します．

• \(N\) が奇数のとき
  • \(N=3\)：\((1,2,3,1)\)
  • \(N=5\)：\((1,2,3,1,4,2,5,3,4,5,1)\)
  • \(N=7\)：\((1,2,3,1,4,2,5,1,6,2,7,3,4,5,3,6,4,7,5,6,7,1)\)

• \(N\) が偶数のとき
  • \(N=2\)：\((1,2)\)
  • \(N=4\)：\((1,2,3,1,4,2,3,4)\)
  • \(N=6\)：\((1,2,3,1,4,2,3,4,5,1,6,2,5,3,6,4,5,6)\)

実装方法について，オイラー路を貪欲に構築してよいことを利用すると場合分けが少なく済んで楽です．計算量は \(O(N^2)\) や \(O(N^3)\) です．

import sys
sys.setrecursionlimit(10**5)

def dfs(v):
    for u in range(n):
        if edge[v][u] > 0:
            edge[v][u] -= 1
            edge[u][v] -= 1
            dfs(u)
    trail.append(v)

T = int(input())
for _ in range(T):
    n = int(input())
    edge = [[int(i != j) for j in range(n)] for i in range(n)]
    if n % 2 == 0:
        for i in range(1, n - 1, 2):
            edge[i][i + 1] += 1
            edge[i + 1][i] += 1
    trail = []
    dfs(0)
    print(*[i + 1 for i in trail[::-1]])