 /
/ 
Time Limit: 6 sec / Memory Limit: 1024 MiB
Score: 100 points
Problem Statement
You are given an undirected graph G with 2^N + 1 vertices and 2^{N+1} - 1 edges. The vertices are numbered 0, 1, \dots, 2^N, and the edges are numbered 1, 2, \dots, 2^{N+1}-1.
Each edge in G belongs to one of N+1 types, ranging from type 0 to type N.
For type i (0 \le i \le N), there are exactly 2^i edges, which are numbered 2^i+0, 2^i+1, \dots, 2^i+(2^i-1). The edge numbered 2^i + j (0 \leq j \leq 2^i - 1) is an undirected edge of length C_{2^i + j} that connects vertex j \times 2^{N-i} and vertex (j+1) \times 2^{N-i}.
For example, when N = 3, G looks like the following graph:
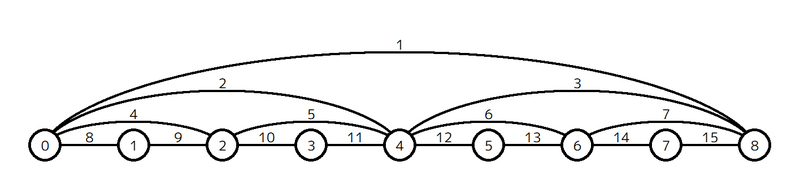
You are given Q queries to process. There are two types of queries:
1 j x: Change the length of edge j to x.2 s t: Find the shortest path length from vertex s to vertex t.
Constraints
- All input values are integers.
- 1 \le N \le 18
- 1 \le C_j \le 10^7 (1 \le j \le 2^{N+1}-1)
- 1 \le Q \le 2 \times 10^5
- In the query
1 j x, 1 \le j \le 2^{N+1}-1 and 1 \le x \le 10^7. - In the query
2 s t, 0 \le s < t \le 2^N. - There is at least one
2 s tquery.
Partial Score
30 points will be awarded for passing the testset satisfying the additional constraint: There is no 1 j x query.
Input
The input is given in the following format. Note that vertex numbering starts from 0, while edge numbering starts from 1.
N
C_1 C_2 \cdots C_{2^{N+1}-1}
Q
\text{query}_1
\text{query}_2
\vdots
\text{query}_Q
Here, \text{query}_i represents the i-th query. Each query is given in one of the following formats:
1 j x
2 s t
Output
Let m be the number of queries of type 2 s t. Output m lines, where the i-th line contains the answer to the i-th 2 s t query.
Sample Input 1
3 7 1 14 3 9 4 8 2 6 5 5 13 8 2 3 10 2 0 1 2 0 4 2 4 6 2 4 8 2 3 5 1 6 30 2 3 5 2 4 6 1 1 10000000 2 0 8
Sample Output 1
2 1 4 8 17 18 13 15
- In the 1st query, using edge 8, the path 0 \to 1 results in a total distance of 2.
- In the 2nd query, using edge 2, the path 0 \to 4 results in a total distance of 1.
- In the 3rd query, using edge 6, the path 4 \to 6 results in a total distance of 4.
- In the 4th query, using edges 2, 1, the path 4 \to 0 \to 8 results in a total distance of 8.
- In the 5th query, using edges 11, 6, 13, the path 3 \to 4 \to 6 \to 5 results in a total distance of 17.
- In the 6th query, the length of edge 6 is updated from 4 to 30.
- In the 7th query, using edges 11, 12, the path 3 \to 4 \to 5 results in a total distance of 18.
- In the 8th query, using edges 2, 1, 15, 14, the path 4 \to 0 \to 8 \to 7 \to 6 results in a total distance of 13.
- In the 9th query, the length of edge 1 is updated from 7 to 10000000.
- In the 10th query, using edges 2, 3, the path 0 \to 4 \to 8 results in a total distance of 15.
配点 : 100 点
問題文
2^N + 1 頂点 2^{N+1} - 1 辺の無向グラフ G が与えられます。頂点には 0, 1, \dots, 2^N の番号が、辺には 1, 2, \dots, 2^{N+1}-1 の番号が割り振られています。
G の辺にはタイプ 0 からタイプ N までの N+1 個の種類があります。
タイプ i (0 \le i \le N) の辺は全部で 2^i 本あり、番号 2^i+0, 2^i+1, \dots, 2^i+(2^i-1) が割り当てられています。番号 2^i + j (0 \le j \le 2^i-1) の辺は、頂点 j \times 2^{N-i} と頂点 (j+1) \times 2^{N-i} を結ぶ長さ C_{2^i + j} の無向辺です。
例えば N = 3 の場合、G は以下のようなグラフになります。

Q 個のクエリが与えられるので、順に処理してください。与えられるクエリには以下の 2 種類があります。
1 j x: 辺 j の長さを x に変更する。2 s t: 頂点 s から頂点 t への最短経路の長さを求める。
制約
- 入力はすべて整数
- 1 \le N \le 18
- 1 \le C_j \le 10^7 (1 \le j \le 2^{N+1}-1)
- 1 \le Q \le 2 \times 10^5
1 j xのクエリにおいて、1 \le j \le 2^{N+1}-1 かつ 1 \le x \le 10^7 である2 s tのクエリにおいて、0 \le s < t \le 2^N である2 s tのクエリが 1 つ以上存在する
部分点
以下の制約を満たすデータセットに正解した場合は 30 点が与えられる。
1 j xのクエリが存在しない
入力
入力は以下の形式で与えられる。頂点番号は 0 から始まるのに対し、辺番号は 1 から始まることに注意せよ。
N
C_1 C_2 \cdots C_{2^{N+1}-1}
Q
\text{query}_1
\text{query}_2
\vdots
\text{query}_Q
ここで、\text{query}_i は i 個目のクエリを表す。各クエリは以下のいずれかの形式で与えられる。
1 j x
2 s t
出力
2 s t のクエリの個数を m として、m 行出力せよ。そのうち i 行目には、i 個目の 2 s t のクエリの答えを出力せよ。
入力例 1
3 7 1 14 3 9 4 8 2 6 5 5 13 8 2 3 10 2 0 1 2 0 4 2 4 6 2 4 8 2 3 5 1 6 30 2 3 5 2 4 6 1 1 10000000 2 0 8
出力例 1
2 1 4 8 17 18 13 15
- 1 個目のクエリでは、辺 8 を用いて 0 \to 1 と移動することで最短距離 2 を達成できます。
- 2 個目のクエリでは、辺 2 を用いて 0 \to 4 と移動することで最短距離 1 を達成できます。
- 3 個目のクエリでは、辺 6 を用いて 4 \to 6 と移動することで最短距離 4 を達成できます。
- 4 個目のクエリでは、辺 2, 1 を用いて 4 \to 0 \to 8 と移動することで最短距離 8 を達成できます。
- 5 個目のクエリでは、辺 11, 6, 13 を用いて 3 \to 4 \to 6 \to 5 と移動することで最短距離 17 を達成できます。
- 6 個目のクエリでは、辺 6 の長さを 4 から 30 に変更します。
- 7 個目のクエリでは、辺 11, 12 を用いて 3 \to 4 \to 5 と移動することで最短距離 18 を達成できます。
- 8 個目のクエリでは、辺 2, 1, 15, 14 を用いて 4 \to 0 \to 8 \to 7 \to 6 と移動することで最短距離 13 を達成できます。
- 9 個目のクエリでは、辺 1 の長さを 7 から 10000000 に変更します。
- 10 個目のクエリでは、辺 2, 3 を用いて 0 \to 4 \to 8 と移動することで最短距離 15 を達成できます。