Choose the point with the smallest \(y\)-coordinate as \(v_1\), and let us only count the subsets \(S\) such that \(v_1 \in S\).

Let \(S\) and \(T = (V \setminus S)\) both be valid sets, and let the polygons determined by \(S\) and \(T\) be \(C_S\) and \(C_T\), respectively. For simplicity, assume \(S, T \neq \emptyset\).

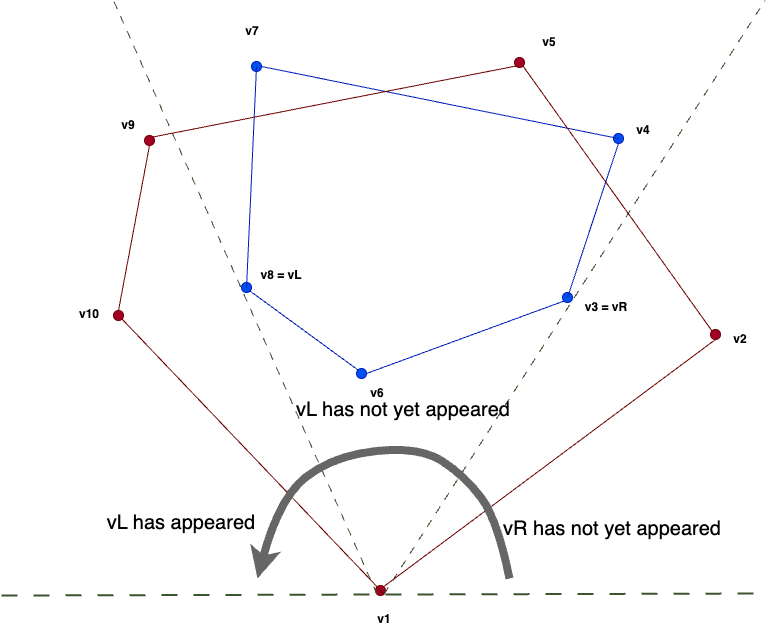
Sort the vertices of \(V\) in counterclockwise order around \(v_1\), and let the sequence of vertices be \(v = (v_1, v_2, v_3, \dots, v_N)\). In this case, the sequence of vertices of \(C_S\) starting from \(v_1\) and arranged counterclockwise is a subsequence of \(v\).

The same applies to \(T\). Let the first vertex of \(T\) appearing in \(v\) be \(v_R\), and the last vertex be \(v_L\). Divide \(C_T\) into its upper convex hull \(C_u\) and lower convex hull \(C_d\) by splitting \(C_T\) with the line segment \(v_Lv_R\). Here, \(C_u\) refers to the side farther from \(v_1\), and \(C_d\) refers to the side closer to \(v_1\) (for convenience, both \(v_L\) and \(v_R\) are considered to belong to both sides). In this case, the sequence of vertices of \(C_u\) arranged counterclockwise from \(v_R\) to \(v_L\) is a subsequence of \(v\), and the sequence of vertices of \(C_d\) arranged clockwise from \(v_R\) to \(v_L\) is also a subsequence of \(v\). Based on this, the following DP can be considered:

Compute the number of ways to appropriately assign \(v_1, v_2, \dots, v_i\) to one of \(C_S\), \(C_u\), or \(C_d\) such that the state is either \(v_R\) has not yet appeared / \(v_R\) has appeared but \(v_L\) has not yet appeared / \(v_L\) has appeared, and the information of at most the last two vertices assigned to \(C_S\), \(C_u\), or \(C_d\) is represented as \(I\) (so-called “ears DP” in Japan).

With just the information of at most the last two vertices assigned, it is possible to count only those polygons that remain convex.

Although \(I\) appears to have \(O(N^6)\) states, by categorizing how \(v_{i-1}\) and \(v_i\) are assigned into \(9\) cases, the number of states can be reduced to \(O(N^4)\).

By implementing this properly, a solution with a time complexity of \(O(N^5)\) can be achieved. Be mindful of space complexity. The intended solution is implemented using a 64-bit integer array of size approximately \(18N^4\). Note that since DP transitions occur only from \(i\) to \(i+1\), a memory reduction by a factor of \(1/N\) is possible.