\(y\) 座標の最も小さな点を \(1\) つ取って \(v_1\) とします。また \(v_1\in S\) となる \(S\) のみを数えることにします。

\(S,T=(V\setminus S)\) がともに良い集合であるとし、 \(S,T\) が定める多角形を \(C_S,C_T\) とします。ここでは簡単のため \(S,T\neq \emptyset\) とします。

\(v_1\) を中心に反時計回りの偏角ソートをして \(V\) の頂点が \(v=(v_1,v_2,v_3,\dots ,v_{N})\) の順に現れるとします。このとき \(C_S\) の頂点を \(v_1\) から始めて反時計回りに並べた列は \(v\) の部分列になっています。

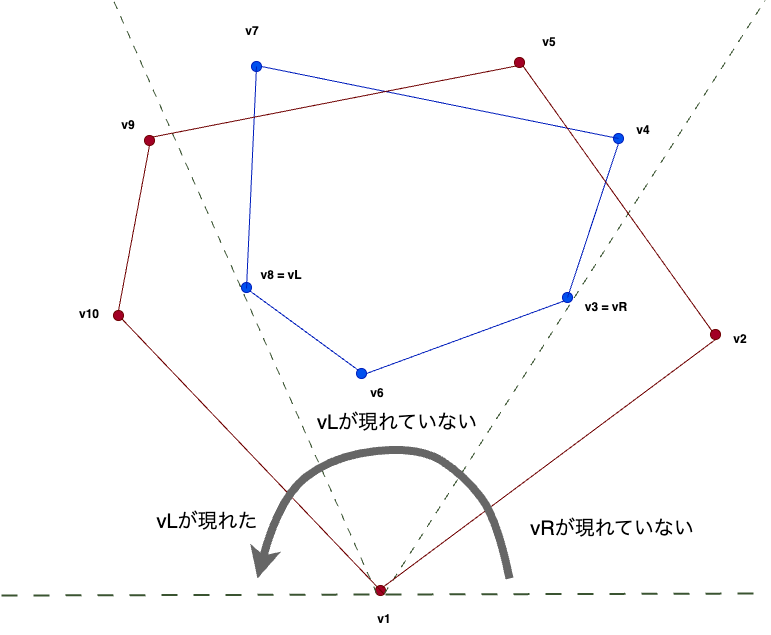
\(T\) についても同様のことが成り立ちます。 \(T\) の頂点で \(v\) 上で最初に現れる頂点を \(v_R\) 、最後に現れる頂点を \(v_L\) します。 \(C_T\) の 上側凸包 \(C_u\) と 下側凸包 \(C_d\) を \(C_T\) を直線 \(v_Lv_R\) で分けたときの \(v_1\) から遠い側と近い側とします（ 便宜上 \(v_L,v_R\) はいずれにも属することにします）。このとき \(C_T\) の上側凸包を \(v_R\) から始めて \(v_L\) まで反時計回りに並べた列は \(v\) の部分列になっています。また、 \(C_T\) の下側凸包を \(v_R\) から始めて \(v_L\) まで 時計回り に並べた列は \(v\) の部分列になっています。そこで、次のようなDPを考えることができます。

\(v_1,v_2,\dots ,v_i\) を \(C_S,C_u,C_d\) のいずれかに適切に割り当て、 \(v_R\) がまだ現れていない/ \(v_R\) は現れたが \(v_L\) が現れていない/ \(v_L\) が現れた状態であり（耳DPの要領）、直前に \(C_S,C_u,C_d\) に割り当てた高々 \(2\) 頂点の情報が \(I\) であるようなものの個数を計算する

直前に割り当てた高々 \(2\) 頂点の情報さえあれば、多角形が凸になるものだけを数えることができます。

\(I\) は \(O(N^6)\) 個の状態を持っているように見えますが、 \(v_{i-1},v_i\) をいずれに割り当てたかを \(9\) 通りに場合分けして持つことで \(O(N^4)\) 個の状態に圧縮することができます。

以上を適切に実装することで \(O(N^5)\) 時間の解法が得られます。空間計算量に気をつけてください。想定解は大きさが \(18N^4\) 程度の \(64\) bit 整数の配列を用いて実装しています。DP の遷移が \(i\to i+1\) しか起こっていないことから \(1/N\) 倍のメモリ削減ができることに注意してください。