J - Set Construction 解説
by  shobonvip
shobonvip
ストーリー
この解説は問題の背景を述べたものです。
あらすじ:Set Construction を有限位相空間の問題に言い換えます。その後、有限位相空間と前順序という順序との関係を述べます。最後に、公式解説の解法をグラフで表すという内容になっています。
解法については公式解説:解説や公式解説:別解をご覧ください。
位相空間
\(X\) を空でない集合とします。 \(X\) の部分集合全体の集合を \(2^X\) とします。 \(2^X\) の部分集合(つまり \(X\) のいくつかの部分集合の集合) \(\mathcal{O}\) が \(X\) の開集合系 (system of open sets) であるとは、
- \(\emptyset \in \mathcal{O}\)
- \(X \in \mathcal{O}\)
- \((O_\lambda)_{\lambda \in \Lambda}\) は \(\mathcal{O}\) の元からなる任意の集合族(添字集合 \(\Lambda\) は任意, 無限集合でもよい)とすると、和集合 \(\cup_{\lambda \in \Lambda} O_{\lambda} \in \mathcal{O}\)
- \(O_1, O_2 \in \mathcal{O}\) ならば \(O_1 \cap O_2 \in \mathcal{O}\)
をすべて満たすことを言います。 \(\mathcal{O}\) の元を開集合 (open set) と言います。 \((X, \mathcal{O})\) の組のことを位相空間と言います。
\(\mathcal{O}\) の無限集合族の和集合が必ず開集合になるのに対して、 共通部分は必ずしも開集合にならないことに注意してください。しかし、 \(X\) が有限空間だと、条件は以下でよいです。
- \(\emptyset \in \mathcal{O}\)
- \(X \in \mathcal{O}\)
- \(O_1, O_2 \in \mathcal{O}\) ならば \(O_1 \cup O_2 \in \mathcal{O}\)
- \(O_1, O_2 \in \mathcal{O}\) ならば \(O_1 \cap O_2 \in \mathcal{O}\)
有限集合における位相空間を有限位相空間と言います。
Set Construction をもう一度見てみます。 \(X = \{0, 1, \cdots, N-1\}\) とします。条件を満たす \(A\) から \(2^X\) への写像 \(f: A \to 2^X\) を、 \(a \in A\) について、 \(a\) の bit が立っている \(2^i\ (0 \le i < N)\) の \(i\) 全体の集合に対応させるものとします。そうすると、 \(X\) の開集合系ができます。
そうすると、Set Construction の問題は次のように言い換えられます:
- 要素数 \(N\) の有限位相空間であって、その開集合系の要素数が \(M\) であるようなものを求めよ。
有限位相空間と前順序 (preorder) との関係
有限位相空間と、 前順序という二項関係とには、一対一の対応(全単射)があります。
前順序(擬順序、preorder)とは、反射律と推移律を満たす二項関係です。すなわち、 \(P\) を集合、 \(\le\) を二項関係とすると、
- [反射律] \(P\) の任意の元 \(a\) に対して、 \(a \le a\) が成り立つ
- [推移律] \(P\) の任意の元 \(a, b, c\) に対し、 \(a \le b\) かつ \(b \le c\) なら \(a \le c\) が成り立つ
がともに成り立つ順序です。前順序に対して、追加で反対称律が成り立つと半順序(partial order) と言い、半順序に対して、追加で全順序律が成り立つと全順序(total order)と言います。(参考: 順序集合 - Wikipedia)
有限位相空間 \((X, \mathcal{O})\) があったとき、 \(X\) に対して次のように前順序を定めることができます:
- \(a, b \in X\) であるとき、 \(a \le b\) であることは、「任意の \(\mathcal{O}\) の要素 \(O\) について、 \(a \in O\) ならば \(b \in O\) が成り立つ」とき、かつそのときに限る
これが前順序になる証明
[反射律] \(a \in O\) なら \(a \in O\) は常に成り立つので、明らかです。
[推移律] \(a, b, c \in X\) について、 \(a \le b\) かつ \(b \le c\) が成り立っているとします。\(O \in \mathcal{O}\) を任意にとり、 \(a \in O\) であるとします。
このとき、 \(a \le b\) より \(b \in O\) 、そして \(b \le c\) より \(c \in O\) です。よって、 \(a \in O\) なら、 \(c \in O\) が成り立ちます。
\(O \in \mathcal{O}\) は任意だったので、 \(a \le c\) です。
これによって、「 \(X\) における位相空間全体の集合」から、「 \(X\) に定まる前順序」への写像 \(f\) が定まりますが、これは全単射となっています。
全単射の証明 準備:写像をつくる
【写像をつくる】 逆写像を構成します。「 \(X\) に定まる前順序」から「 \(X\) における位相空間全体の集合」への写像 \(g\) を以下のように定めます:
まず、 \(a \in X\) に対し、 \(a \le b\) を満たす \(b \in X\) の集合を \(T_a\) とします。写像 \(T: 2^X \to 2^X\) を次のように定めます。
- ある \(X\) の部分集合 \(S\) が与えられたとき、それに対応する集合 \(T(S)\) を、 \(T(S) = \cup_{a \in S} T_a\) とする。ただし、 \(T(\emptyset) = \emptyset\) とする。
\(X\) の部分集合 \(S\) にすべてについての \(T(S)\) の和集合を \(\mathcal{O}\) とします。すなわち、
\[ \mathcal{O} = \cup_{S \in 2^X} T(S) = \cup_{S \in 2^X} \left(\cup_{a \in S} T_a\right) \]
とします。このとき、 \((X, \mathcal{O})\) は有限位相空間になっていることが以下のように確認されます。
[ \(\emptyset, X\) を含むこと] \(T(S)= \emptyset\) 、 \(T(S) = X\) になるので、成り立ちます。
[和集合] \(O_1, O_2 \in \mathcal{O}\) のとき、 \(T(S_1) = O_1, T(S_2) = O_2\) となる \(O_1, O_2\) が存在するので、それを \(1\) 個とります。
\[ \begin{aligned} \displaystyle O_1 \cup O_2 &= T(S_1) \cup T(S_2)\\ &= \left(\cup_{a \in S_1} T_a\right) \cup \left(\cup_{b \in S_2} T_b\right)\\ &= \cup_{a \in (S_1 \cup S_2)} T_a\\ &= T(S_1 \cup S_2) \end{aligned} \]
ですが、 \(T(S_1 \cup S_2) \in \mathcal{O}\) なので成り立ちます。
[共通部分] 和集合と同様で、 \(O_1 \cap O_2 = T(S_1 \cap S_2) \in \mathcal{O}\) が示されます。
全単射の証明 前半戦:\(g \circ f\) が恒等写像になっていること
開集合系 \(\mathcal{O}\) があったとき、 \(g(f(\mathcal{O})) = \mathcal{O}\) を示します。
前順序 \(f(\mathcal{O})\) を考えます。 \(a \in X\) を固定します。 \(a \le b\) を満たす \(b \in X\) の集合は、定義より、 \(O \in \mathcal{O}\) であって、 \(a \in O\) を満たすものすべての共通部分になります。
\(g(f(\mathcal{O})) = \mathcal{O}\) を示すために、包含関係 \(g(f(\mathcal{O})) \subset \mathcal{O}\) と \(g(f(\mathcal{O})) \supset \mathcal{O}\) を示します。
以下、写像 \(T\) 、集合 \(T_a\) は「準備:写像をつくる」で使われたものと同様とします。
【 \(g(f(\mathcal{O})) \subset \mathcal{O}\) 】 \(O' \in g(f(\mathcal{O}))\) とします。ある \(X\) の部分集合 \(S\) が存在して、 \(O' = T(S) = \cup_{a \in S} T_a\) です。
さきほど述べたときの、「 \(O \in \mathcal{O}\) であって、 \(a \in O\) を満たすものすべての共通部分」は、開集合系の定義より開集合です。
よって、各 \(a \in X\) に対して、 \(T_a\) は \(\mathcal{O}\) の開集合です。よってそのいくつかの和集合である \(O' = T(S) = \cup_{a \in S} T_a\) も \(\mathcal{O}\) の開集合になっています。
よって、 \(O' \in \mathcal{O}\) が示されました。以上から、 \(g(f(\mathcal{O})) \subset \mathcal{O}\) が示されました。
【 \(g(f(\mathcal{O})) \supset \mathcal{O}\) 】 \(O' \in \mathcal{O}\) とします。 このとき、 \(g(f(\mathcal{O}))\) において \(T(O')\) を考えます。
\(T(O') = \cup_{a \in O'} T_a\) は \(a \le a\) なので \(O'\) を含みます。よって \(O' \subset T(O')\) です。
逆も示します。 \(f\) の定義により \(a \in O'\) に対して \(T_a \subset O'\) が成り立つので、 \(T(O') = \cup_{a \in O'} T_a \subset O'\) です。
以上から、 \(T(O') = O'\) です。これより、とくに \(T(O') \in g(f(\mathcal{O}))\) が従います。よって、 \(g(f(\mathcal{O})) \supset \mathcal{O}\) です。
【まとめ】 \(g(f(\mathcal{O})) \subset \mathcal{O}\) 、 \(g(f(\mathcal{O})) \supset \mathcal{O}\) がともに成り立つので、 \(g(f(\mathcal{O})) = \mathcal{O}\) です。よって、 \(g \circ f\) は恒等写像であることが示されました。
全単射の証明 後半戦:\(f \circ g\) が恒等写像になっていること
\(D\) を \(X\) における前順序とします。 前順序 \(D\) における順序を \(\le_1\) 、前順序 \(f(g(D))\) における順序を \(\le_2\) とします。証明するべきことは、任意の \(a,b \in X\) に対して \(a \le_1 b \Leftrightarrow a \le_2 b\) です。
【 \(a \le_1 b \Rightarrow a \le_2 b\) 】 \(a \le_1 b\) とします。 \(O \in g(D)\) を任意として、 \(a \in O\) なら、ある \(S \in 2^X\) が存在して \(T(S) = O\) です。
いま、 \(a \in T_c\) となる \(c \in S\) が存在しますが、 \(c \le_1 a\) であるので推移律より \(T_a \subset T_c\) です。よって、 \(a \le_1 b\) より \(b \in T_a\) 、すなわち \(b \in T_c\) です。 \(O\) は任意だったので \(f\) の定義より \(a \le_2 c\) が成り立ちます。
【 \(a \le_2 b \Rightarrow a \le_1 b\) 】 \(a \le_2 b\) とします。任意の \(O \in g(D)\) に対して、 \(a \in O\) なら \(b \in O\) が成り立ちます。\(a \in T_a\) であるので、 \(b \in T_a\) が従います。
いま、 \(a \le_1 b\) でないとすると、 \(b \not \in T_a\) となるので矛盾します。よって、 \(a \le_1 b\) です。
上の「全単射の証明」より、前順序は次の性質を満たします:
- \(a \in X\) に対し、 \(a \le b\) を満たす \(b \in X\) の集合を \(T_a\) とする。ある \(X\) の部分集合 \(S\) が与えられたとき、それを含む(集合の包含に関して)最小の開集合を \(T\) とすると、 \(T = \cup_{a \in S} T_a\) となる
(参考:有限集合上の位相 - Motoo Tange’s Blog)
グラフで表してみよう
要素数 \(N\) の集合における有限位相空間と前順序と一対一対応があるので、 頂点数 \(N\) の有向グラフであって、「 \(a \le b\) であるとき、かつそのときに限り \(a\) から \(b\) に到達可能である」というものが存在します。ここだけの単語ですが、これを、位相空間を表すグラフと言うこととします。(一般的な単語ではないことに注意してください)
ある \(X\) の部分集合 \(S\) が与えられたとき、それを含む最小の開集合を \(T\) とすると、 \(T\) は \(S\) のいずれかの点から到達可能な点全体の集合です。すなわち、開集合系は、
\[\cup_{S \in 2^X} (S のいずれかの点から到達可能な点全体)\]
となります。
例
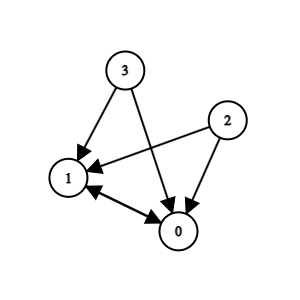
\(N = 4, M = 5\) を満たす \(A = \{0, 3, 7, 11, 15\}\) は、開集合系とすると \(\{\emptyset, \{0, 1\}, \{0, 1, 2\}, \{0, 1, 3\}, \{0, 1, 2, 3\}\}\) です。
\(a \le b\) を満たす \(a, b \in \{0, 1, 2, 3\}\) についてすべての辺を貼ると、これは位相空間を表すグラフで、自己ループを除いて以下の通りになります。
到達可能であればよいので、以下も位相空間を表すグラフになります。
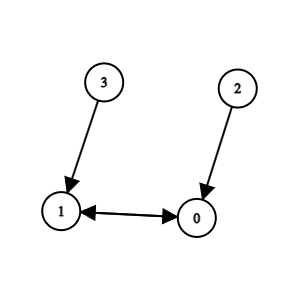
たとえば、\(S = \{2\}\) とすると、 \(2\) から到達可能な点の集合は \(\{0, 1, 2\}\) なので、 \(S\) を含む最小の開集合は \(\{0, 1, 2\}\) と計算できます。
\(S = \emptyset\) とすると、 \(\emptyset\) から到達可能な点の集合は \(\emptyset\) です。
いま、 \(0, 1\) は相互に繋がれていますが、これによって反対称律が成り立っていないため、半順序ではありません。
脱線
要素数 \(N\) の集合における有限位相空間の個数を求める公式はまだ見つかっていません。
- 同型のものを重複して数える:A000798 - OEIS
- 有限位相空間は前順序と一対一対応があるので、それを数え上げる問題にもなります。
- 同型のものを重複せずに数える:A001930 - OEIS
- 同型のものを重複して数える:A000798 - OEIS
有限位相空間は前順序と一対一対応になりますが、他の二項関係はどうなるでしょうか。
- 半順序については有限 \(T_0\)-位相空間と一対一対応があります。
- 同値関係については有限 \(\sigma\)-加法族と一対一対応があります。
- 似た話題の問題: yukicoder No.2134 \(\sigma\)-algebra over Finite Set
- 似た話題の問題: Codeforces 908E - New Year and Entity Enumeration(確認していません、参考:競技プログラミングにおける数学的問題まとめ - はまやんはまやんはまやん の「σ加法族とベル数の関連性 」より)
- 要素数 \(N\) の有限 \(\sigma\)-加法族の個数は同型のものを重複して数えるとベル数(リンクはWikipedia)、同型のものを重複せず数えると分割数(リンクはWikipedia)となり、簡単に求められます。
解説をグラフで考える
公式解説:解説のように、 \(f(N,M)\) を \(N, M\) の場合の答えとします。以下に解説する内容は、グラフの図を除けば、公式解説:別解 とほとんど同じです。
\(f(N-1,M)\) から \(f(N,M)\) を構成する
\(A = f(N-1, M)\) として、
\[B = \{2a + (a \% 2) ~ | ~ a \in A\}\]
とすると、この \(B\) は条件を満たします。これを位相空間を表すグラフで表すと、
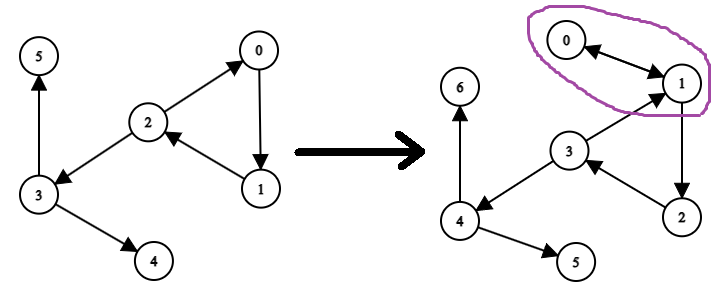
このようになります。新しいグラフでは、頂点 \(0, 1\) は同値である(開集合において属するか否かが同期している)と考えられます。開集合系の要素数は \(f(N-1, M)\) と同一になることが直感的に分かります。
直積
位相同士の直積を考えることができます。\((X, \mathcal{O}_X), (Y, \mathcal{O}_Y)\) を位相空間とします。集合の直積
\[X \times Y = \{(A, B) \mid A \in X, B \in Y\}\]
\[\mathcal{O}_X \times \mathcal{O}_Y = \{(A, B) \mid A \in \mathcal{O}_X, B \in \mathcal{O}_Y\}\]
によって、 \((X \times Y, \mathcal{O}_X \times \mathcal{O}_Y)\) は位相空間となります。このとき、開集合系の要素数は \(|\mathcal{O}_X| |\mathcal{O}_Y|\) となり、 \(f(n_1, m_1)\) と \(f(n_2, m_2)\) から \(f(n_1n_2, m_1m_2)\) を構成することができます。
\(M\) が偶数のとき \(f(N-1,M/2)\) から \(f(N, M)\) を構成する
\(A = f(N-1, M/2), B = \{1\}\) とします。
\[C = \{2a + b ~ | ~ a \in A, b \in B\}\]
とすると、この \(C\) は条件を満たします。これを位相空間を表すグラフで表すと、

このようになります。新しいグラフは、 \(f(N-1, M/2)\) と \(f(1,1)\) の位相の直積となっていることが分かります。
\(N = 5\) かつ \(M = 15\) のとき
\(A = f(2, 3), B = f(3, 5)\) とします。
\[C = \{8a + b ~ | ~ a \in A, b \in B\}\]
とすると、この \(C\) は条件を満たします。これを位相空間を表すグラフで表すと、

このようになります。新しいグラフは、 \(f(2, 3)\) と \(f(3, 5)\) の位相の直積となっていることが分かります。
上下につなげる
\((X, \mathcal{O}_X), (Y, \mathcal{O}_Y)\) を位相空間とします。ただし、\(X, Y\) は互いに素とします。 \(\mathcal{O}\) を、
\[\mathcal{O} = \mathcal{O}_X \cup \{X \cup B \mid B \in \mathcal{O}_Y\}\]
とすると、 \((X \cup Y, \mathcal{O})\) は位相空間となります。このとき、 \(\mathcal{O}_X\) と \(\{X \cup B \mid B \in \mathcal{O}_Y\}\) は唯一 \(X\) のみを共通の要素として持つので、開集合系の要素数は \(|\mathcal{O}_X| + |\mathcal{O}_Y| - 1\) となり、 \(f(n_1, m_1)\) と \(f(n_2, m_2)\) から \(f(n_1 + n_2, m_1 + m_2 - 1)\) を構成することができます。
\(f(N-1,M-1)\) から \(f(N, M)\) を構成する
\(A = f(N-1, M-1)\) とします。
\[C = \{2a + 1 ~ | ~ a \in A, b \in B\} \cup \{0\}\]
とすると、この \(C\) は条件を満たします。これを位相空間を表すグラフで表すと、

このようになります。新しいグラフは、 \(f(1,2)\) ( \(A = \{0, 1\}\) ) と \(f(N-1, M-1)\) の位相を「つなげた」ものだと考えることができます。
参考
投稿日時:
最終更新:
