D - EMLauncher 解説
by  t98slider
t98slider
公式解説の計算量\(O(N ^ {2})\)の解法について簡単に説明した後、より高速な計算量\(O(N \log N)\)の解法について説明します。
\(O(N^{2})\)解法
まず、この問題の性質として、原点から見た際に重ならないように選んだ線分(障害物)の個数の最大値がすべての線分(障害物)を破壊するために必要な試射の回数の最小値に一致するというものがあります。(後述させて頂きましたが、最大値に言い換えなくても解くことは可能です。)原点から見た際の線分(障害物)が重なっていなければ同時に破壊できず、逆に重なっていれば、重ならない線分(障害物)の集合として選んだものを破壊する過程で同時に破壊することが出来ます。
よって、それぞれの線分について偏角ソートしたものに対し、それぞれの線分を始点とした際の区間スケジューリング問題を解くことで本問題を\(O(N^{2})\)で解くことができます。
以下は実装の一例についての説明です。
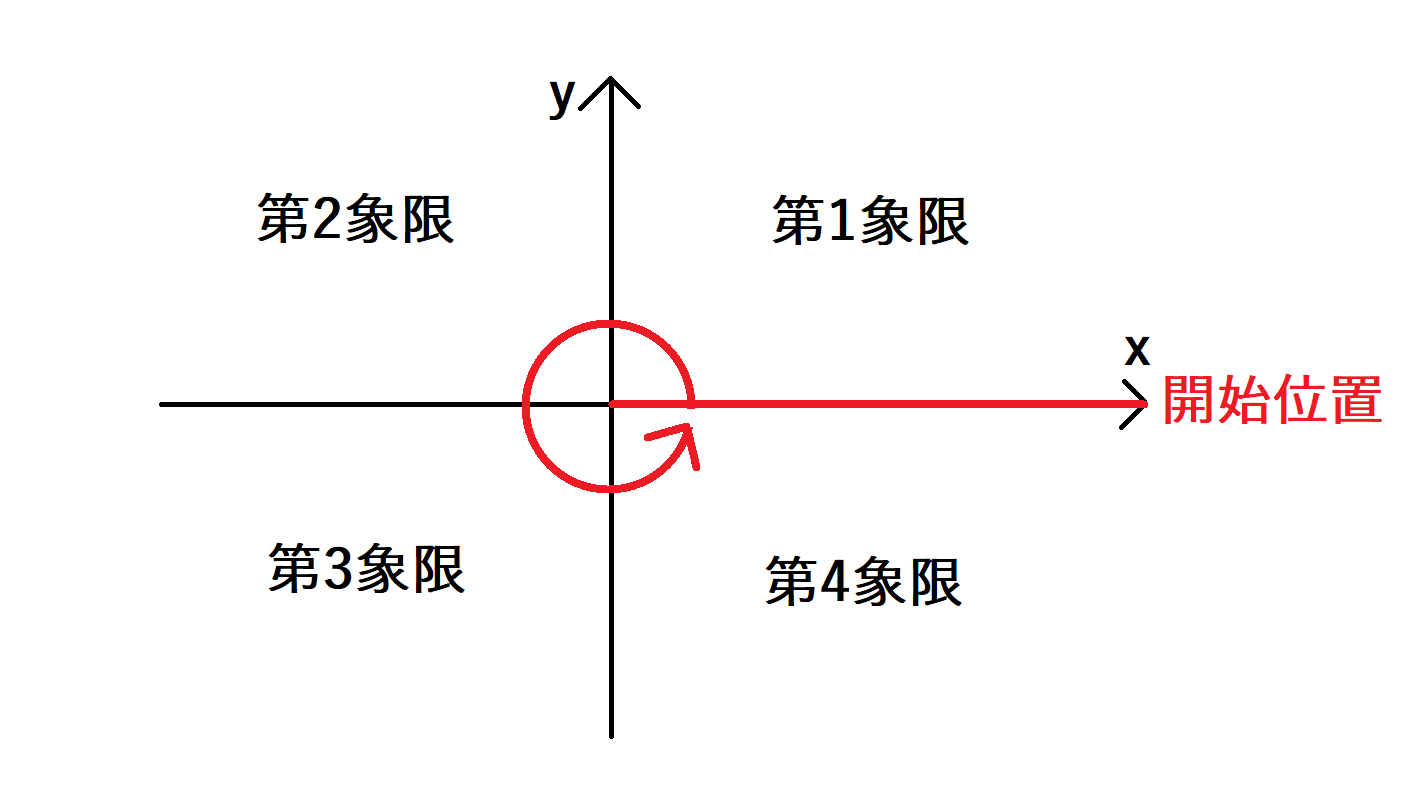
偏角ソートについて\(x\)軸正の向きの半直線を開始位置として反時計回りに偏角ソートを行います。まず、それぞれの点(位置ベクトル)について第1象限、第2象限、第3象限、第4象限に分類します。
続いて、位置ベクトルのベクトルの外積について計算をします。2次元のベクトルの外積は、2つのベクトルを \(\vec{a} =[a_{x}, a_{y}]\) 、ベクトル \(\vec{b}=[b_{x},b_{y}]\) とすると、
\[ \vec{a} \times \vec{b} = a_{x} b_{y} - a_{y} b_{x} \]
で計算されます。外積が正となるとき、\(\vec{b}\) は \(\vec{a}\) に対して反時計回りにあり、外積が負となるとき \(\vec{b}\) は \(\vec{a}\) に対して時計回りにあります。外積が零となる場合は、 \(\vec{a}\) と \(\vec{b}\) は同一直線上にあり、 \(\vec{a}\) と \(\vec{b}\) が同じ方向を向いているか反対方向を向いているかを判定する必要が出て来ますが、今回は先に4つの象限について分類を行ったので、同じ方向を向いていると考えることができます。
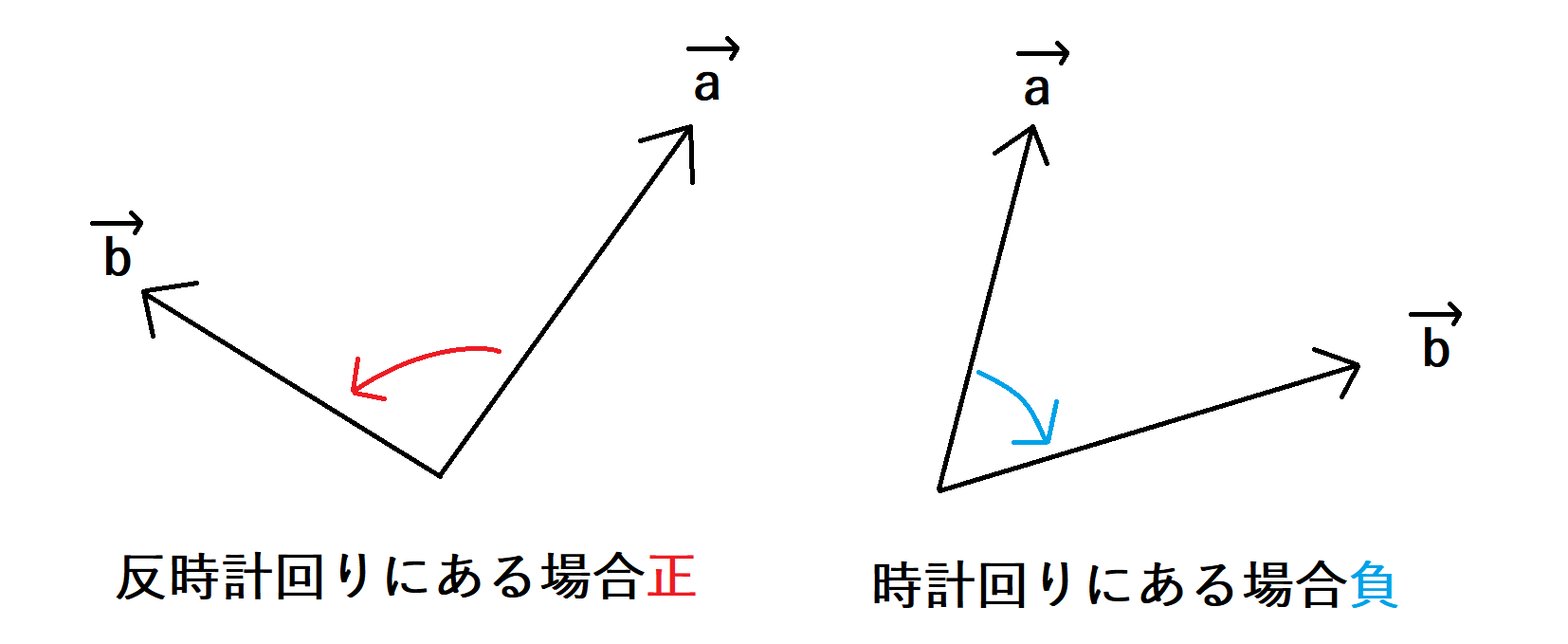
以上、ベクトル\(\vec{a}\)、\(\vec{b}\)の比較についてまとめると、
- \(\vec{a}\) が第\(i\)象限に属していて、 \(\vec{b}\) が第\(j\) 象限に属しているとする。
- \(i < j\)ならば、\(\vec{a}\) の方が小さい
- \(i > j\)ならば、\(\vec{b}\) の方が小さい
- \(i = j\)のとき、\(\vec{a} \times \vec{b} > 0\) ならば、\(\vec{a}\) の方が小さい
- \(i = j\)のとき、\(\vec{a} \times \vec{b} < 0\) ならば、\(\vec{b}\) の方が小さい
- \(i = j\)のとき、\(\vec{a} \times \vec{b} = 0\) ならば、同一のベクトルと見なす
struct point{
int x, y;
friend bool operator < (const point &lhs, const point &rhs){
int lo = (lhs.y > 0 ? (lhs.x >= 0 ? 1 : 2) : (lhs.x < 0 ? 3 : 4));
int ro = (rhs.y > 0 ? (rhs.x >= 0 ? 1 : 2) : (rhs.x < 0 ? 3 : 4));
if(lo != ro)return (lo < ro);
return (lhs.x * rhs.y - lhs.y * rhs.x > 0);
}
};
続いて、偏角のままだと扱いずらいので、数直線上の区間に変換します。イメージとしては下図のような感じです。
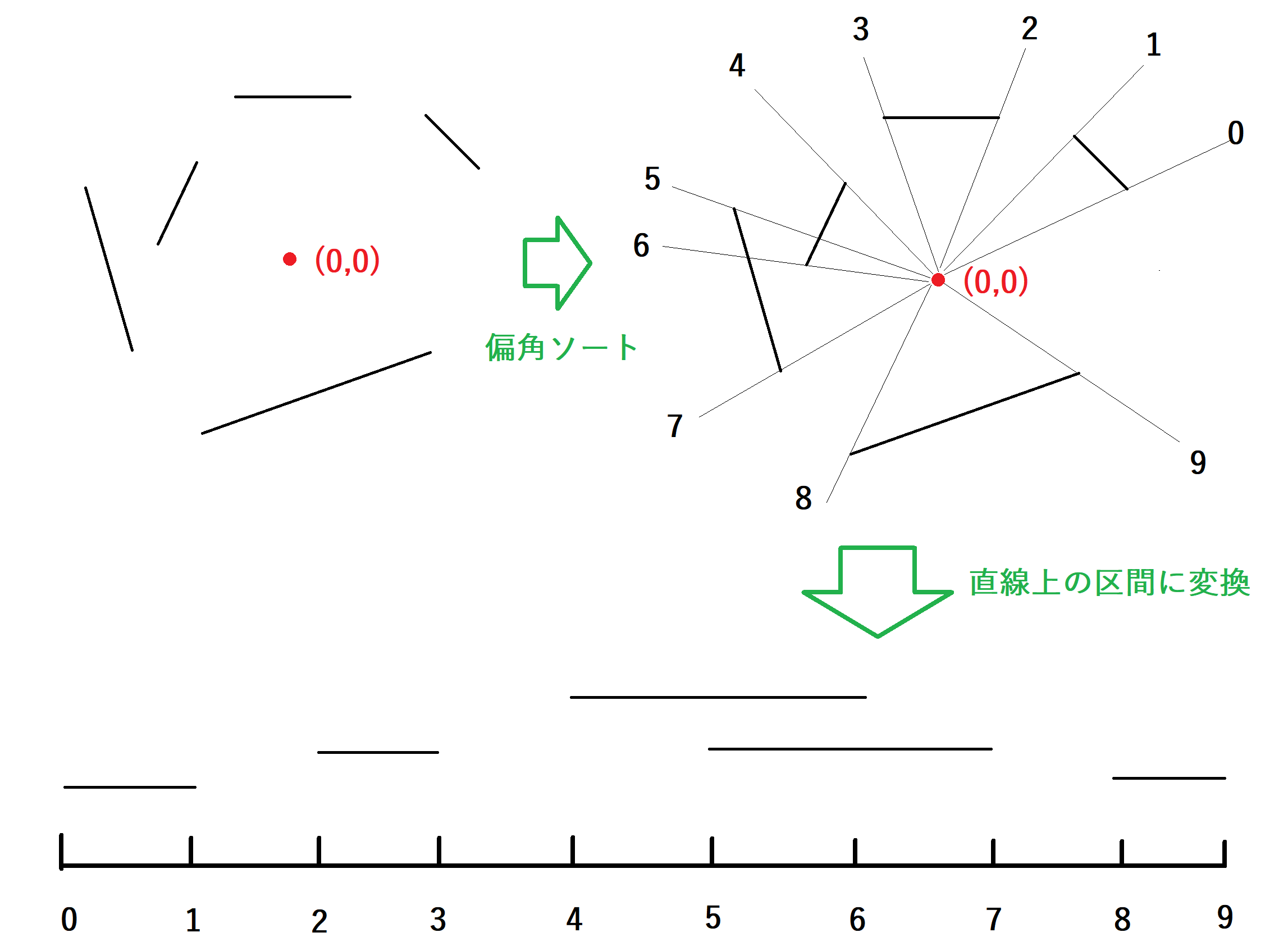
区間の左端に対応するベクトルを\(\vec{L}\) 、右端に対応するベクトルを\(\vec{R}\) とします。\(\vec{R}\) が\(\vec{L}\)に対して反時計回りの位置にあるとすると、
\[ \vec{L} \times \vec{R} = L_{x} R_{y} - L_{y} R_{x} \geq 0 \]
が成り立ちます。位置ベクトル\(\vec{L}\)、\(\vec{R}\) と原点\(O\)を結ぶ三角形を考えると、角\({\rm LOR}\)はどのような場合でも180度を超えないため、\(\vec{L}\) が\(\vec{R}\) よりも偏角ソートで先に来るベクトルであるとすると、外積は0以上となります。問題の制約で、原点に接したり、原点が端点となったりすることはないようですので、\(\vec{L}\) と\(\vec{R}\) が同じ向きを向いているときだけ外積が0となり、他の場合は\(\vec{L}\)と \(\vec{R} \) を一意に定めることができます。
偏角から数直線上の区間に変換する際に注意するべき点は以下の2点です。
- 円形のものを考えるので2周した区間を用意しておく。
- \(\vec{L}\) に対応する数直線上のindexを\(l\) 、\(\vec{R}\) に対応する数直線上のindexを\(r\) とすると、\(r < l\)となっているものが現れる場合がある。この場合は、\(r\) に一周分の点の数だけ加算しておく。
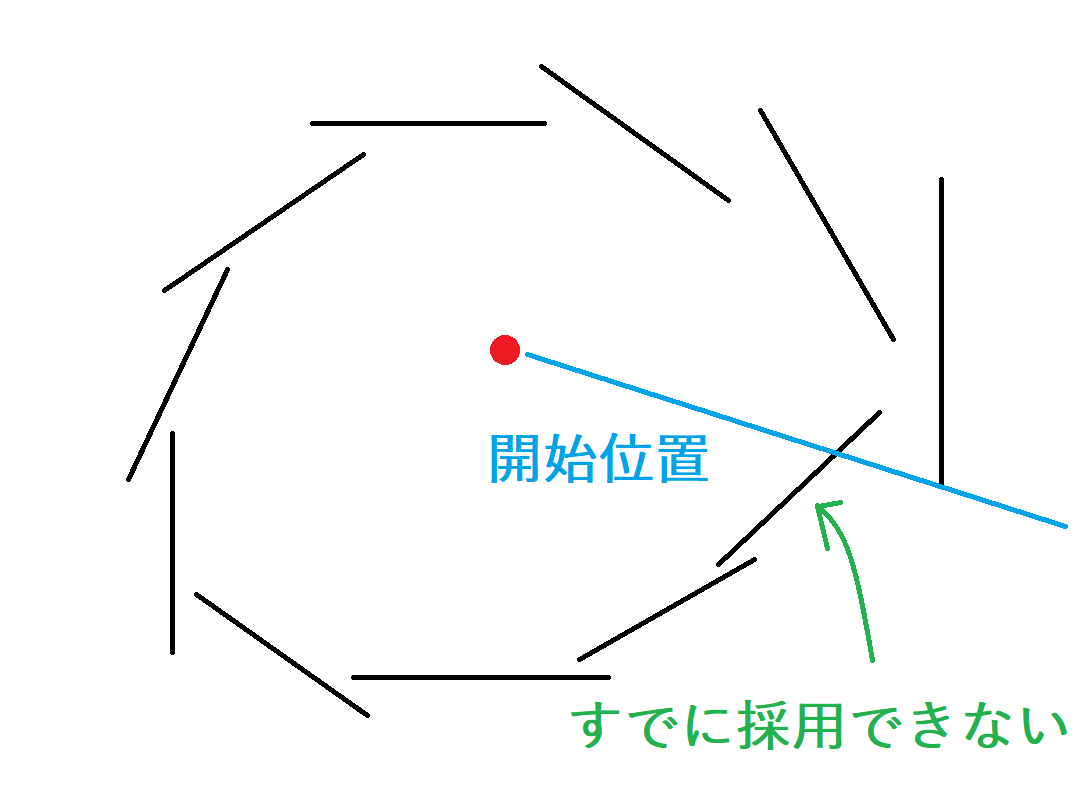
あとは、円弧状の区間スケジューリング問題を解いて、区間の最大数を答えとします。円弧状の区間スケジューリングの場合は、ある区間の開始位置がある区間ですでに選べないような状態となっている場合があります。そこで、一周分の区間を決め打って、すべての開始位置について区間スケジューリング問題を解くことで被らない区間の最大数を求めることができます。
実装例(C++)
#include<bits/stdc++.h>
using namespace std;
struct point{
int x, y;
friend bool operator < (const point &lhs, const point &rhs){
int lo = (lhs.y > 0 ? (lhs.x >= 0 ? 1 : 2) : (lhs.x < 0 ? 3 : 4));
int ro = (rhs.y > 0 ? (rhs.x >= 0 ? 1 : 2) : (rhs.x < 0 ? 3 : 4));
if(lo != ro)return (lo < ro);
return (lhs.x * rhs.y - lhs.y * rhs.x > 0);
}
};
int main(){
int N;
cin >> N;
vector<point> L(N), R(N), C(2 * N);
for(int i = 0; i < N; i++){
cin >> L[i].x >> L[i].y >> R[i].x >> R[i].y;
if(L[i].x * R[i].y - L[i].y * R[i].x < 0)swap(L[i], R[i]);
C[2 * i] = L[i];
C[2 * i + 1] = R[i];
}
sort(C.begin(), C.end());
vector<pair<int,int>> seg(2 * N);
for(int i = 0; i < N; i++){
int l = lower_bound(C.begin(), C.end(), L[i]) - C.begin();
int r = lower_bound(C.begin(), C.end(), R[i]) - C.begin();
if(r < l)r += 2 * N;
seg[2 * i] = {r, l};
seg[2 * i + 1] = {r + 2 * N, l + 2 * N};
}
sort(seg.begin(), seg.end());
int ans = 0;
for(int i = 0; i < N; i++){
int cnt = 0, right = -1, end_pos = seg[i].second + 2 * N;
for(int j = 0; j < N; j++){
int l, r;
tie(r, l) = seg[i + j];
if(r >= end_pos)break;
if(l > right){
right = r;
cnt++;
}
}
ans = max(ans, cnt);
}
cout << ans << '\n';
}
区間スケジューリングとの対比のため\(\vec{L}\)を開始位置として区間の最大数を求める方針で説明しましたが、\(\vec{L}\)ではなく、\(\vec{R}\) を開始位置としてみることで最大数ではなく、区間の最小数を求める方針のまま解くことも可能です。(最適値でない場合は、選んだ区間に被りが生じていることになります。) この場合、決め打った一周分の区間に\(N\)個の線分の\(\vec{R}\)に対応するindexがすべて含まれるようにしておきたいので、数直線上の区間に変換にする際に\(\vec{L}\) が \(\vec{R}\) よりも大きいものが出現したら\(\vec{L}\)に対応するindexから一周分の点の数だけ減算しておくこととなります。
実装例(C++)
#include <bits/stdc++.h>
using namespace std;
struct point{
int x, y;
friend bool operator < (const point &lhs, const point &rhs){
int lo = (lhs.y > 0 ? (lhs.x >= 0 ? 1 : 2) : (lhs.x < 0 ? 3 : 4));
int ro = (rhs.y > 0 ? (rhs.x >= 0 ? 1 : 2) : (rhs.x < 0 ? 3 : 4));
if(lo != ro)return (lo < ro);
return (lhs.x * rhs.y - lhs.y * rhs.x > 0);
}
};
int main(){
int N;
cin >> N;
vector<point> L(N), R(N), C(2 * N);
for(int i = 0; i < N; i++){
cin >> L[i].x >> L[i].y >> R[i].x >> R[i].y;
if(L[i].x * R[i].y - L[i].y * R[i].x < 0)swap(L[i], R[i]);
C[2 * i] = L[i];
C[2 * i + 1] = R[i];
}
sort(C.begin(), C.end());
vector<pair<int,int>> seg(2 * N);
for(int i = 0; i < N; i++){
int l = lower_bound(C.begin(), C.end(), L[i]) - C.begin();
int r = lower_bound(C.begin(), C.end(), R[i]) - C.begin();
if(r < l)l -= 2 * N;
seg[2 * i] = {r, l};
seg[2 * i + 1] = {r + 2 * N, l + 2 * N};
}
sort(seg.begin(), seg.end());
int ans = N;
for(int i = 0; i < N; i++){
int cnt = 0, right = -3 * N;
for(int j = 0; j < N; j++){
int l, r;
tie(r, l) = seg[i + j];
if(right >= l)continue;
right = r;
cnt++;
}
ans = min(ans, cnt);
}
cout << ans << '\n';
}
\(O(N\log N)\)解法
実はこの問題は、数直線上の区間に変換さえしてしまえば、プログラミングコンテストチャレンジブック第2版の307ページの例題にある巡回スケジューリング問題に言い換えることができます。プログラミングコンテストチャレンジブック第2版の307ページの問題は、一週間に見るアニメの本数を最大化する問題でAtCoder上にもほとんど同じ問題があります。 問題へのURL本問題では、以下のようなdp配列を持ちます。
\[ dp[i][j] = 位置jから開始して2^{i}個の区間を被らないように選んだ時の最小の終了位置 \]
与えられる障害物の個数は\(N \leq 2000\)でしたので、\(2 ^ { 11} = 2048\)あれば十分です。このようなダブリングを行うことで、決め打った円弧上の一周分の範囲に対して二分探索することができ、\(O(\log N)\)で被りなく選べる区間の数が求められます。よって、それぞれの一周分の範囲について二分探索を行うことで、全体で\(O(N\log N)\)で被りなく選べる区間の最大数を求めることが出来ます。
実装例(C++)
#include <bits/stdc++.h>
using namespace std;
struct point{
int x, y;
friend bool operator < (const point &lhs, const point &rhs){
int lo = (lhs.y > 0 ? (lhs.x >= 0 ? 1 : 2) : (lhs.x < 0 ? 3 : 4));
int ro = (rhs.y > 0 ? (rhs.x >= 0 ? 1 : 2) : (rhs.x < 0 ? 3 : 4));
if(lo != ro)return (lo < ro);
return (lhs.x * rhs.y - lhs.y * rhs.x > 0);
}
};
int main(){
int N;
cin >> N;
vector<point> L(N), R(N), C(2 * N);
for(int i = 0; i < N; i++){
cin >> L[i].x >> L[i].y >> R[i].x >> R[i].y;
if(L[i].x * R[i].y - L[i].y * R[i].x < 0)swap(L[i], R[i]);
C[2 * i] = L[i];
C[2 * i + 1] = R[i];
}
sort(C.begin(), C.end());
vector<vector<int>> dp(12, vector<int>(4 * N + 1, 4 * N));
for(int i = 0; i < N; i++){
int l = lower_bound(C.begin(), C.end(), L[i]) - C.begin();
int r = upper_bound(C.begin(), C.end(), R[i]) - C.begin();
if(r <= l)r += 2 * N;
dp[0][l] = min(dp[0][l], r);
dp[0][l + 2 * N] = min(dp[0][l + 2 * N], r + 2 * N);
}
for(int j = 4 * N - 1; j >= 0; j--){
dp[0][j] = min(dp[0][j], dp[0][j + 1]);
}
for(int i = 1; i < 12; i++){
for(int j = 0; j < 4 * N; j++){
dp[i][j] = dp[i - 1][dp[i - 1][j]];
}
}
int ans = 0;
for(int l = 0; l < 2 * N; l++){
int r = l + 2 * N, cnt = 0;
for(int i = 11, j = l; i >= 0; i--){
if(dp[i][j] <= r){
j = dp[i][j];
cnt |= 1 << i;
}
}
ans = max(ans, cnt);
}
cout << ans << '\n';
}
類題
偏角ソートしたものに対して区間スケジューリングを行う類題として以下のものがあります。ABC225「E - フ」
投稿日時:
最終更新:
