層 \(N\)（最下層）の各ブロック \(C_{N,i}\) について、そのブロックが \(C_{1,1}\) に与える寄与を計算することを考えます。

一般に \(C_{i,j}\) は層 \(i-1\) に対して \(C_{i-1,j-1}\) と \(C_{i-1,j}\) の \(2\) つのブロックに影響を与えます。このとき、 \(C_{i-1,j-1}\) に対しては係数 \(1\) で、 \(C_{i-1,j}\) に対しては係数 \(10^{2^{N-i}}\) で寄与します。

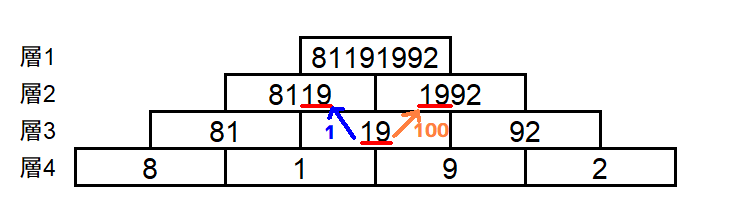
\(C_{i,j}\) は層 \(i-1\) に寄与するとき、\(C_{i-1,j-1}\) と \(C_{i-1,j}\) に寄与することの \(2\) 択があると考え、 \(C_{i-1,j-1}\) に寄与することを「左上に進む」、 \(C_{i-1,j}\) に寄与することを「右上に進む」と言うことにします。

この「左上に進む」または「右上に進む」という寄与を繰り返すと、必ず \(C_{1,1}\) に到達します。そして、 \(C_{N,i}\) のブロックは必ず「左上に進む」回数が \(i-1\) 回、「右上に進む」回数が \(N-i\) 回であることが分かります。

逆に、「左上に進む」回数が \(i-1\) 回、「右上に進む」回数が \(N-i\) 回であるような進み方は \(C_{N,i}\) から \(C_{1,1}\) への寄与として妥当であることも分かります。

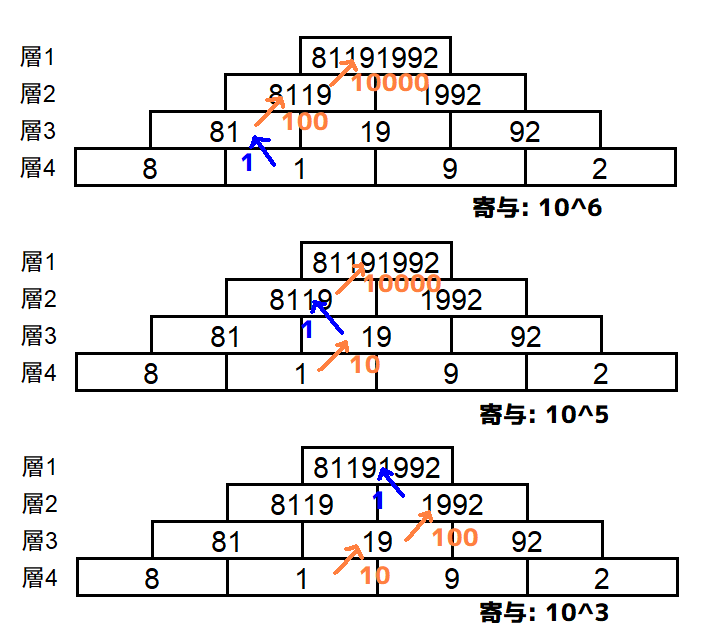
さて、これを多項式で表現してみます。「右上に進む」たびに \(x\) が掛けられるとすると、 \(C_{N,i}\) から \(C_{1,1}\) への寄与の合計は、

\[C_{N,i} [x^{N-i}] \prod_{t=1}^{N-1} (1+10^{2^{t-1}}x)\]

となります。すべての \(i\) についてこれを求めるためには、多項式 \(\prod_{t=1}^{N-1} (1+10^{2^{t-1}}x)\) の展開を求めればよく、多項式マージテク（分割統治）を用いることで \(O(N \log^2 N)\) 時間で実現できます。